
分析 (1)求出实验发生包含的事件是3位申请人中,满足条件的所有事件有43种结果.恰有1人申请A片区房源结果,然后求解概率.
(2)ξ的所有可能结果为0,1,2,3,求出概率,得到X的分布列然后求解期望即可.
解答 解:(1)本题是一个等可能事件的概率,实验发生包含的事件是3位申请人中,
每一个有四种选择,共有43种结果.
满足条件的事件恰有1人申请A片区房源有$C_3^1•{3^2}$,
根据等可能事件的概率$p=\frac{{c_3^1{3^2}}}{4^3}=\frac{27}{64}$.
(2)ξ的所有可能结果为0,1,2,3,依题意,$p({ξ=0})=\frac{3^3}{4^3}=\frac{27}{64}$,$p({ξ=1})=\frac{{c_3^1•{3^2}}}{4^3}=\frac{27}{64}$,$p({ξ=2})=\frac{c_3^2•3}{4^3}=\frac{9}{64}$,$p({ξ=3})=\frac{1}{4^3}=\frac{1}{64}$,
∴X的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
点评 本题考查概率的求法,二项分布的分布列以及期望的求法,考查转化思想以及计算能力.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
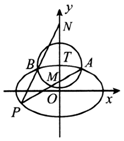 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [-1,2) | C. | (-1,2] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com