
分析 (1)曲线C1化为ρ2=ρcosθ-ρsinθ,由此能求出曲线C1的直角坐标方程.
(2)曲线C1,C2联立,得${t}^{2}+\frac{\sqrt{2}}{2}t-\frac{1}{4}$=0,设t1,t2为方程${t^2}+\frac{{\sqrt{2}}}{2}t-\frac{1}{4}=0$的两根,由此能求出|PQ|的值.
解答 解:(1)∵曲线C1:ρ=cosθ-sinθ,
∴ρ2=ρcosθ-ρsinθ⇒x2+y2=x-y,
∴曲线C1的直角坐标方程为:x2+y2-x+y=0…(5分)
(2)∵曲线${C_2}:\left\{{\begin{array}{l}{x=\frac{1}{2}-\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$(t为参数),
∴联立$\left\{{\begin{array}{l}{{x^2}-x+{y^2}+y=0}\\{x=\frac{1}{2}-\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$,得${t}^{2}+\frac{\sqrt{2}}{2}t-\frac{1}{4}$=0,
设t1,t2为方程${t^2}+\frac{{\sqrt{2}}}{2}t-\frac{1}{4}=0$的两根,则$\left\{{\begin{array}{l}{{t_1}+{t_2}=-\frac{{\sqrt{2}}}{2}}\\{{t_1}{t_2}=-\frac{1}{4}}\end{array}}\right.$,
∴$|PQ|=|{t_1}-{t_2}|=\sqrt{{{({t_1}+{t_2})}^2}-4{t_1}{t_2}}=\frac{{\sqrt{6}}}{2}$.…(10分)
点评 本题考查曲线的直角坐标方程的求法,考查线段长的求法,是中档题,解题时要认真审题,注意极坐标方程与直角坐标方程的互化公式的合理运用.


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
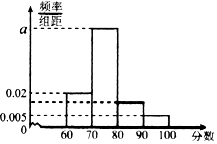 某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:
某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [60,70) | 16 | 0.2 |
| [70,80) | 50 | n |
| [80,90) | 10 | P |
| [90,100] | 4 | 0.05 |
| 合计 | M | I |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>c>a | B. | c>b>a | C. | b>a>c | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008 | B. | 1010 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2) | B. | [-1,+∞) | C. | (2,3] | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com