
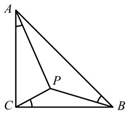
 如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )
如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 可得△ABP∽△BCP⇒$\frac{AP}{PB}=\frac{PB}{PC}=\frac{AB}{BC}=\sqrt{2}$,即AP=$\sqrt{2}PB$,PC=$\frac{1}{\sqrt{2}}PB$,由∠ACP+∠PCB=90°,∠PCB=∠CAP,∠CPA=90°,tan$α=tan∠CAP=\frac{PC}{PA}$=$\frac{1}{\sqrt{2}}PB×\frac{1}{\sqrt{2}PB}=\frac{1}{2}$.
解答  解:在等腰直角三角形ABC中,∠C是直角,且∠CAP=∠BCP=∠ABP=α,
解:在等腰直角三角形ABC中,∠C是直角,且∠CAP=∠BCP=∠ABP=α,
∴∠CBP=∠PAC,⇒△ABP∽△BCP⇒$\frac{AP}{PB}=\frac{PB}{PC}=\frac{AB}{BC}=\sqrt{2}$
∴AP=$\sqrt{2}PB$,PC=$\frac{1}{\sqrt{2}}PB$,
∵∠ACP+∠PCB=90°,∠PCB=∠CAP,∴∠ACP+∠CAP=90°,∴∠APC=90°
tan$α=tan∠CAP=\frac{PC}{PA}$=$\frac{1}{\sqrt{2}}PB×\frac{1}{\sqrt{2}PB}=\frac{1}{2}$.
故选:A.
点评 本题考查了解三角形,考查了转化思想,属于中档题,


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
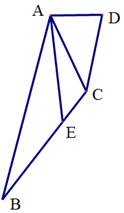 在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.
在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
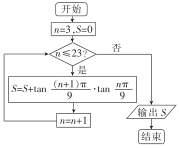
| A. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$ | B. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | ||
| C. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | D. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
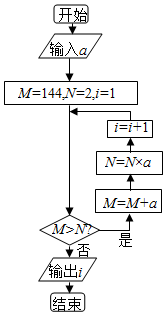 执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )
执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )| A. | [9,+∞) | B. | [8,9] | C. | [8,144) | D. | [9,144) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
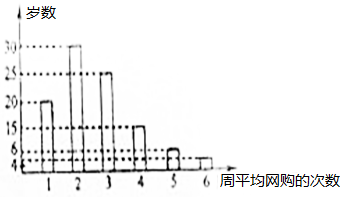 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | |||
| 年龄超过40岁 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com