
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用几何概型的概率公式得到关于m 的等式解之即可.根据区间[-1,3]的长度为4,可得当x满足|x|≤m的概率为时0.75,x所在的区间长度为3.解不等式|x|≤m得解集为[-m,m],从而得到[-m,m]与[-1,3]的交集为[-1,2],由此可解出m的值
解答 解:∵区间[-1,3]的区间长度为3-(-1)=4,
∴随机地取一个数x,若x满足|x|≤m的概率为0.75,
则满足条件的区间长度为4×0.75=3.
因此x所在的区间为[-1,2],
∵m>0,得|x|≤m的解集为{m|-m≤x≤m}=[-m,m],
∴[-m,m]与[-1,3]的交集为[-1,2]时,可得m=2.
故选:C.
点评 本题给出几何概型的值,求参数m.着重考查了绝对值不等式的解法、集合的运算和几何概型计算公式等知识.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知a>1,?x>0,ax≤1 | B. | $已知0<a<1,?{x_0}<0,{a^{x_0}}≤1$ | ||
| C. | $已知0<a<1,?{x_0}≥0,{a^{x_0}}≤1$ | D. | 已知a>1,?x>0,ax≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{3}$ | C. | $\frac{8}{3}\sqrt{2}$ | D. | $\frac{4}{3}\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∨q | C. | (¬p)∧q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,1] | D. | [-1,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
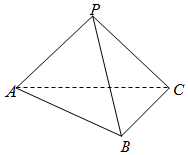 如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.
如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com