
| A. | (-$\frac{1}{2}$,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,1] | D. | [-1,$\frac{1}{2}$) |
分析 将已知的等式变形,能够得到A的范围,然后求sin(2A+$\frac{π}{6}$)取值范围.
解答 解:因为$\frac{b}{c}$=$\frac{cosA}{1+cosC}$,由正弦定理得到$\frac{sinB}{sinC}=\frac{cosA}{1+cosC}$,
所以sinCcosA=sin(A+C)(1+cosC),
展开整理得到cosC(sinA+sinB)=0,因为sinA+sinB≠0,所以cosC=0,所以C=$\frac{π}{2}$,
所以A+B=$\frac{π}{2}$,所以0<A<$\frac{π}{2}$,所以$\frac{π}{6}$<2A+$\frac{π}{6}$<$\frac{7π}{6}$,所以-$\frac{1}{2}$<sin(2A+$\frac{π}{6}$)≤1;
所以sin(2A+$\frac{π}{6}$)的取值范围是(-$\frac{1}{2}$,1];
故选B
点评 本题考查了正弦定理的运用以及三角函数值域的求法;关键是由已知求出A的范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
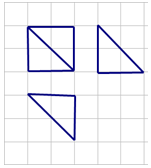
| A. | $8+4\sqrt{2}$ | B. | $6+4\sqrt{2}$ | C. | 12 | D. | $8+5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{2}-θ$ | B. | $θ-\frac{π}{2}$ | C. | $\frac{π}{2}+θ$ | D. | θ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
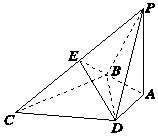 如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com