
 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.分析 (1)利用椭圆C过点$(2,\frac{{4\sqrt{3}}}{3})$,右准线方程为x=6,a2=b2+c2,列出方程组求解即可.
(2)设M(x1,y1),N(x2,y2),则A(-a,0),B(a,0),F(c,0);求出MA,MB的斜率乘积,
设直线MN:x=my+c,与椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,通过韦达定理推出${k_{BM}}•{k_{BN}}=-\frac{b^4}{{{a^2}{{(a-c)}^2}}}$,结合2kMA=kBN;即可求解椭圆C的离心率.
解答 (本小题满分16分)
解:(1)因为椭圆C过点$(2,\frac{{4\sqrt{3}}}{3})$,所以$\frac{4}{a^2}+\frac{16}{{3{b^2}}}=1$,
又已知右准线方程为x=6,所以$\frac{a^2}{c}=6$,a2=b2+c2,
可解得a2=12,b2=8;或a2=28,${b^2}=\frac{56}{9}$;
所以椭圆C的方程为$\frac{x^2}{12}+\frac{y^2}{8}=1$或$\frac{x^2}{28}+\frac{{9{y^2}}}{56}=1$.(6分)
(2)设M(x1,y1),N(x2,y2),则A(-a,0),B(a,0),F(c,0);
因为点M在椭圆C上,所以$y_1^2={b^2}(1-\frac{x_1^2}{a^2})=-\frac{b^2}{a^2}(x_1^2-{a^2})$,
所以${k_{MA}}•{k_{MB}}=\frac{y_1}{{{x_1}+a}}•\frac{y_1}{{{x_1}-a}}=\frac{y_1^2}{{x_1^2-{a^2}}}=-\frac{b^2}{a^2}$,
设直线MN:x=my+c,与椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$联立方程组消去x得(a2+m2b2)y2+2cmb2y-b4=0,${k_{BM}}•{k_{BN}}=\frac{y_1}{{{x_1}-a}}•\frac{y_2}{{{x_2}-a}}=\frac{y_1}{{m{y_1}+c-a}}•\frac{y_2}{{m{y_2}+c-a}}$=$\frac{{{y_1}{y_2}}}{{{m^2}{y_1}{y_2}+m(c-a)({y_1}+{y_2})+{{(c-a)}^2}}}$,
将${y_1}{y_2}=-\frac{b^4}{{{a^2}+{m^2}{b^2}}}$,${y_1}+{y_2}=-\frac{{2cm{b^2}}}{{{a^2}+{m^2}{b^2}}}$代入上式化简得${k_{BM}}•{k_{BN}}=-\frac{b^4}{{{a^2}{{(a-c)}^2}}}$,又2kMA=kBN;所以$-\frac{{2{b^2}}}{a^2}=-\frac{b^4}{{{a^2}{{(a-c)}^2}}}$,
得a2-4ac+3c2=0,即3e2-4e+1=0,解得$e=\frac{1}{3}$或e=1,
又0<e<1,所以$e=\frac{1}{3}$,即椭圆C的离心率为$\frac{1}{3}$.(16分)
点评 本题考查直线与椭圆的位置关系的综合应用,椭圆方程的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 已知a>1,?x>0,ax≤1 | B. | $已知0<a<1,?{x_0}<0,{a^{x_0}}≤1$ | ||
| C. | $已知0<a<1,?{x_0}≥0,{a^{x_0}}≤1$ | D. | 已知a>1,?x>0,ax≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,1] | D. | [-1,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
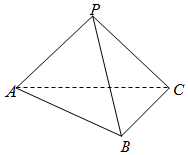 如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.
如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com