
分析 逐个条件进行验证:首先可验证四个函数都满足条件①;对于条件②,若f′(x)的符号容易判断,可验证不等式xf'(x)>0成立,若f′(x)的符号不容易判断,可理解到为函数在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,通过函数的单调性进行判断,可排除不满足条件的g(x)和Φ(x);对剩余的函数验证条件③,h(x)和Φ(x)都在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,所以由条件③可设x1<0<x2,则有h(-x2)-h(x1)=h(-x2)-h(x2),构造函数F(x)=h(-x)-h(x),通过求导判断F(x)在(0,+∞)上的单调性,从而判断F(x2)与F(0)的大小关系,即得到h(-x2)与h(x1)的大小关系,从而得到x1+x2的符号,判断条件③是否成立,函数φ(x)同样的方法来验证条件③.
解答 经验证,g(x),h(x),Φ(x),φ(x)都满足条件①;
xf′(x)>0?$\left\{\begin{array}{l}{x>0}\\{f′(x)>0}\end{array}\right.$,或$\left\{\begin{array}{l}{x<0}\\{f′(x)<0}\end{array}\right.$.即条件②等价于函数f(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增.
而容易验证g(x)是奇函数,由及函数的性质可知g(x)在区间(-∞,0)和(0,+∞)上单调性相同,故g(x)不满足条件②.
由复合函数的单调性法则知h(x)在区间(-∞,0)上单调递减,显然在(0,+∞)上单调递增,故h(x)满足条件②.
Φ′(x)=-3x2+3x,xΦ′(x)=-3x3+3x2=-3x2(x-1),当x>1时,xΦ′(x)<0,故Φ(x)不满足条件②.
φ′(x)=ex-1,xφ′(x)=x(ex-1),满足条件②.
故由条件②可排除g(x)和Φ(x);
由函数h(x)的单调性知:当x1≠x2,且h(x1)=h(x2)时,x1x2<0,不妨设x1<0<x2.
则ln(-x1+1)=2x2,设F(x)=ln(x+1)-2x,x>0.则F′(x)=$\frac{1}{x+1}-2=\frac{-2x-1}{x+1}$<0,F(x)在(0,+∞)上是减函数,
所以F(x2)<F(0)=0,即ln(x2+1)<2x2,即ln(x2+1)<ln(-x1+1),所以x2+1<-x1+1,即x1+x2<0,故h(x)也满足条件③,所以h(x)是“偏对称函数”.
由φ(x)的单调性知当x1≠x2,且φ(x1)=φ(x2)时,x1x2<0,不妨设x1<0<x2.
则${e}^{{x}_{1}}-{x}_{1}-1={e}^{{x}_{2}}-{x}_{2}-1$,-x2<0,φ(x1)-φ(-x2)=φ(x2)-φ(-x2)=${e}^{{x}_{2}}-{e}^{-{x}_{2}}-2{x}_{2}$.
令F(x)=ex-e-x-2x,F′(x)=${e}^{x}+{e}^{-x}-2≥2\sqrt{{e}^{x}•{e}^{-x}}-2=0$,当且仅当ex=e-x即x=0时,“=”成立,
所以F(x)在[0,+∞)上是增函数,所以F(x2)>F(0)=0,即φ(x1)-φ(-x2)>0,所以φ(x1)>φ(-x2),所以x1<-x2,所以x1+x2<0.所以φ(x)是“偏对称函数”.
故答案为:2
点评 本题主要是在新定义下考查函数的单调性与最值、导数的应用,属于难题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. | 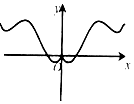 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{9}{2}$π+24 | B. | $\frac{9}{2}$π+30 | C. | 9π+54 | D. | 36π+30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
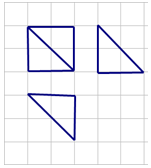
| A. | $8+4\sqrt{2}$ | B. | $6+4\sqrt{2}$ | C. | 12 | D. | $8+5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
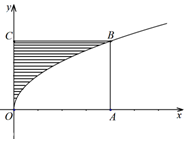 如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com