Question

14．如图，在多面体ABCDEF中，四边形ABCD为正方形，EF∥AB，EF⊥EA，AB=2EF=2，∠AED=90°，AE=ED，H为AD的中点．
（1）求证：EH⊥平面ABCD；
（2）在线段BC上是否存在一点P，使得二面角B-FD-P的大小为$\frac{π}{3}$？若存在，求出BP的长；若不存在，请说明理由．

Answer 1

分析 （1）推导出AB⊥EA，AB⊥AD，从而AB⊥EH，再求出EH⊥AD．由此能证明EH⊥平面ABCD．
（2）由AD，OH，HE两两垂直，建立空间直角坐标系H-xyz，利用向量法能求出结果．

解答 证明：（1）因为AB∥EF，EF⊥EA，所以AB⊥EA．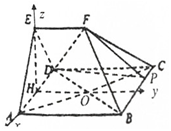
因为AB⊥AD，且EA∩AD=A，所以AB⊥平面AED．
因为EH?平面AED，所以AB⊥EH．
因为AE=ED，H是AD的中点，所以EH⊥AD．
又AB∩AD=A，所以EH⊥平面ABCD．
解：（2）因为AD，OH，HE两两垂直，
如图，建立空间直角坐标系H-xyz，
则A（1，0，0）D（-1，0，0），F（0，1，1），O（0，1，0），C（-1，2，0）．
设点P（m，2，0）（-1≤m＜1），
于是有$\overrightarrow{DF}=（1，1，1）$，$\overrightarrow{DP}=（m+1，2，0）$．
设平面PDF的法向量$\vec n=（x，y，z）$，则$\left\{\begin{array}{l}\vec n•\overrightarrow{DF}=0\\ \vec n•\overrightarrow{DP}=0\end{array}\right.$，即$\left\{\begin{array}{l}x+y+z=0\\（m+1）x+2y=0\end{array}\right.$．
令x=2，得y=-（m+1），z=m-1，所以$\vec n=（2，-m-1，m-1）$．
平面BDF的法向量$\overrightarrow{OA}=（1，-1，0）$，
所以$cos\frac{π}{3}=\frac{{|\overrightarrow{OA}•\vec n|}}{{|\overrightarrow{OA}|•|\vec n|}}$，解得m=-1．
所以点P的坐标为（-1，2，0），
与点C的坐标相同，所以BP=BC=2．

点评 本题考查线面垂直的证明，考查满足条件的点是否存在的判断与求法，是中档题，解题时要认真审题，注意向量法的合理运用．