
| A�� | 0�� | B�� | 45�� | C�� | 90�� | D�� | 180�� |
���� ����������ƽ����Ϊģ��ƽ��������ʽ����ƽ�������ɵõ��нǣ�
��� �⣺����$\overrightarrow a$��$\overrightarrow b$�ļн�Ϊ�ȣ�
��$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$��
��|$\overrightarrow{a}+\overrightarrow{b}$|2=��|$\overrightarrow{a}$|-|$\overrightarrow{b}$|��2��
��|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2|$\overrightarrow{a}$|•|b|��
��2|$\overrightarrow{a}$|•|b|cos��=-2|$\overrightarrow{a}$|•|b|��
��cos��=-1��
���=180��
��ѡ��D
���� ���⿼��ƽ�������������������ʣ�������ƽ����Ϊģ��ƽ���������������������ڻ����⣮


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д� ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
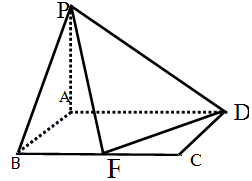 ��ͼ������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��AD=2��AB=1��F���߶�BC���е�
��ͼ������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��AD=2��AB=1��F���߶�BC���е��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x∉R��tanx��1 | B�� | ?x��R��tanx=1 | C�� | ?x0∉Rtanx0=1 | D�� | ?x0��R��tanx0=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
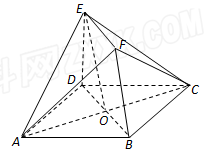 ��ͼ��������ABCD��ֱ������BDEF���ڵ�ƽ�滥�ഹֱ��OΪ������ABCD�����ģ�AD=DE=2$\sqrt{2}$��EF��BD��BD=2EF��DE��BD��
��ͼ��������ABCD��ֱ������BDEF���ڵ�ƽ�滥�ഹֱ��OΪ������ABCD�����ģ�AD=DE=2$\sqrt{2}$��EF��BD��BD=2EF��DE��BD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com