
分析 确定集合A的元素范围,根据A∩B=A,建立条件关系即可求实数a的取值范围.
解答 解:由题意:集合A={x||2x-1|≤3}={x|-1≤x≤2}
集合B={x|x2+(4-a)x-4a>0}={x|(x+4)(x-a)>0},
∵A∩B=A
∴A⊆B.
解法一:
令f(x)=x2+(4-a)x-4a>0,
∵-1≤x≤2,
根据一元二次方程的根的分布:
可得:$\left\{\begin{array}{l}{-\frac{b}{2a}≤-1}\\{f(-1)≥0}\end{array}\right.$或$\left\{\begin{array}{l}{-\frac{b}{2a}≥2}\\{f(2)≥0}\end{array}\right.$
解:a≤-1
故得实数a的取值范围是:(-∞,-1].
解法二,讨论思想:
当a=-4时,B={x∈R|x≠-4},满足A⊆B.
当a>-4时,B={x|x>a或x<-4},
要使A⊆B成立,则:a≤-1.
当a<-4时,B={x|x<a或x>-4},满足A⊆B.
故得实数a的取值范围是:(-∞,-1].
点评 本题考查的知识点是集合的包含关系判断及应用,集合关系中的参数问题,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4] | B. | [0,4] | C. | [0,1] | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 种 | B. | 4 种 | C. | 5 种 | D. | 6 种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$(2n-1) | B. | $\frac{1}{24}$(2n+4) | C. | $\frac{1}{24}$(4n-1) | D. | $\frac{1}{16}$(4n-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
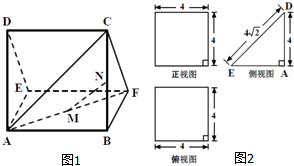
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com