
分析 (1)由三角函数恒等变换的应用化简等式右边,结合已知即可计算得解.
(2)利用β=(α-β)-α,结合两角差的正切函数公式即可计算得解.
(3)利用两角差的正切函数公式计算可求tan(2α-β)=1,结合范围0<2α<$\frac{π}{2}$,$\frac{π}{2}$<β<π,-π<2α-β<0,即可得解.
解答 解:(1)由已知tanα=$\frac{1}{3}$.
∵tan(α-β)=$\frac{sin2(\frac{π}{2}-α)+4co{s}^{2}α}{10co{s}^{2}α+cos(\frac{3π}{2}-2α)}$=$\frac{sin2α+4cos2α}{10cos2α-sin2α}$=$\frac{2sinαcosα+4cos2α}{10cos2α-2sinαcosα}$=$\frac{2cosα?sinα+2cosα?}{2cosα?5cosα-sinα?}$=$\frac{sinα+2cosα}{5cosα-sinα}$=$\frac{tanα+2}{5-tanα}$=$\frac{{\frac{1}{3}+2}}{{5-\frac{1}{3}}}=\frac{1}{2}$.…(3分)
(2)tan β=-tan[(α-β)-α]=-$\frac{tan(α-β)-tanα}{1+tan(α-β)tanα}$=$\frac{{\frac{1}{2}-\frac{1}{3}}}{{1+\frac{1}{2}•\frac{1}{3}}}=-\frac{1}{7}$.…(7分)
(3)∵tan α=$\frac{1}{3}$>0,
∴0<α<$\frac{π}{2}$,
又∵tan 2α=$\frac{2tanα}{1-tan2α}$=$\frac{2×\frac{1}{3}}{1-(\frac{1}{3})^{2}}$=$\frac{3}{4}$>0,
∴0<2α<$\frac{π}{2}$,
∴tan(2α-β)=$\frac{tan2α-tanβ}{1+tan2αtanβ}$=$\frac{\frac{3}{4}+\frac{1}{7}}{1-\frac{3}{4}×\frac{1}{7}}$=1.
∵tan β=-$\frac{1}{7}$<0,
∴$\frac{π}{2}$<β<π,-π<2α-β<0,
∴2α-β=-$\frac{3π}{4}$.…(12分) (如果多个答案,没判断范围扣2分)
点评 本题主要考查了三角函数恒等变换的应用,两角差的正切函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{9},\frac{1}{3})$ | B. | $(-1,-\frac{1}{3})$ | C. | $(-1,-\frac{1}{3})∪(\frac{1}{9},\frac{1}{3})$ | D. | $[{-1,-\frac{1}{3}}]∪[{\frac{1}{9},\frac{1}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,平面PAD⊥底面ABCD.
在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,平面PAD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
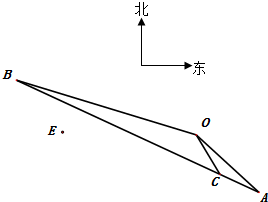 如图,某自行车手从O点出发,沿折线O-A-B-O匀速骑行,其中点A位于点O南偏东45°且与点O相距20$\sqrt{2}$千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°-α)(其中sinα=$\frac{1}{{\sqrt{26}}}$,0°<α<90°)且与点O相距5$\sqrt{13}$千米(假设所有路面及观测点都在同一水平面上).
如图,某自行车手从O点出发,沿折线O-A-B-O匀速骑行,其中点A位于点O南偏东45°且与点O相距20$\sqrt{2}$千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°-α)(其中sinα=$\frac{1}{{\sqrt{26}}}$,0°<α<90°)且与点O相距5$\sqrt{13}$千米(假设所有路面及观测点都在同一水平面上).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{5}$ | D. | $2\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com