
 如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,且底面ABCD是正方形,M为AA1的中点,连接BD,MB,MD,MC1.
如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,且底面ABCD是正方形,M为AA1的中点,连接BD,MB,MD,MC1.分析 (1)连接AC,交BD于点O,连接OM,证明OM∥A1C,即可证明A1C∥平面BDM;
(2)证明AA1⊥BD,AC⊥BD,得出BD⊥平面ACC1A1,从而证明BD⊥MC1.
解答 解:(1)证明:连接AC,交BD于点O,连接OM,如图所示;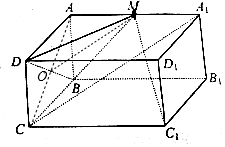
∵底面ABCD是正方形,∴O是AC的中点,
又M为AA1的中点,
∴OM∥A1C,又A1C?平面BDM,OM?平面BDM,
∴A1C∥平面BDM;
(2)证明:由AA1⊥底面ABCD,BD?平面ABCD,
∴AA1⊥BD,
又底面ABCD是正方形,∴AC⊥BD,
且AC∩AA1=A,AC?平面ACC1A1,AA1?平面ACC1A1,
∴BD⊥平面ACC1A1,
又MC1?平面ACC1A1,∴BD⊥MC1.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了推理与证明能力,是中档题.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{24}$ | B. | $\frac{7π}{24}$ | C. | $\frac{5π}{36}$ | D. | $\frac{7π}{36}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段表示通道,并且在交点处相遇,假设一个小弹子在交点处向左或向右是等可能的.若竖直线段有一条的为第一层,有两条的为第二层,…,依此类推,现有一颗小弹子从第一层的通道向下运动.猜想该小弹子落入第n+1层的第m个通道里的概率$\frac{{C}_{n}^{m-1}}{{2}^{n}}$.
如图,是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段表示通道,并且在交点处相遇,假设一个小弹子在交点处向左或向右是等可能的.若竖直线段有一条的为第一层,有两条的为第二层,…,依此类推,现有一颗小弹子从第一层的通道向下运动.猜想该小弹子落入第n+1层的第m个通道里的概率$\frac{{C}_{n}^{m-1}}{{2}^{n}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com