
【题目】函数y= ![]() 的定义域为 , 值域为 .
的定义域为 , 值域为 .
【答案】(1,2)∪(2,+∞);(﹣∞,0)∪(0,+∞)
【解析】解:函数y= ![]() ,
,
其定义域必须满足: ![]() ,
,
解得:x>1且x≠2.
∴函数y= ![]() 的定义域为(1,2)∪(2,+∞).
的定义域为(1,2)∪(2,+∞).
又∵ln(x﹣1)值域为(﹣∞,0)∪(0,+∞),
∴y= ![]() 值域为(﹣∞,0)∪(0,+∞),
值域为(﹣∞,0)∪(0,+∞),
所以答案是:(1,2)∪(2,+∞);(﹣∞,0)∪(0,+∞).
【考点精析】通过灵活运用函数的定义域及其求法和函数的值域,掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的即可以解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位后得到函数
)个单位后得到函数![]() 的图象.若
的图象.若![]() 的图象上各最高点到点
的图象上各最高点到点![]() 的距离的最小值为1,求
的距离的最小值为1,求![]() 的单调增区间.
的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件
②“当x为某一实数时可使![]() ”是不可能事件
”是不可能事件
③“明天顺德要下雨”是必然事件
④“从100个灯泡中取出5个,5个都是次品”是随机事件.
其中正确命题的个数是 ( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
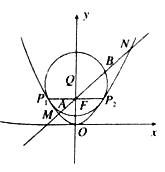
【题目】如图,抛物线![]() 的准线为
的准线为![]() ,取过焦点
,取过焦点![]() 且平行于
且平行于![]() 轴的直线与抛物线交于不同的两点
轴的直线与抛物线交于不同的两点![]() ,过
,过![]() 作圆心为
作圆心为![]() 的圆,使抛物线上其余点均在圆外,且
的圆,使抛物线上其余点均在圆外,且![]() .
.
(Ⅰ)求抛物线![]() 和圆
和圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与抛物线
与抛物线![]() 和圆
和圆![]() 依次交于
依次交于![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销10天,两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.经统计,两个厂家10天的试销情况茎叶图如下:

(Ⅰ)现从厂家试销的10天中抽取两天,求这两天的销售量都大于40的概率;
(Ⅱ)若将频率视作概率,回答以下问题:
(ⅰ)记乙厂家的日返利额为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(ⅱ)商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场做出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于统计数据的分析,有以下几个结论,其中正确的个数为( )
①将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化;
②在线性回归分析中,相关系数r越小,表明两个变量相关性越弱;
③某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人.为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为15人.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2﹣mx(m>0)在区间[0,2]上的最小值记为g(m)
(1)若0<m≤4,求函数g(m)的解析式;
(2)定义在(﹣∞,0)∪(0,+∞)的函数h(x)为偶函数,且当x>0时,h(x)=g(x),若h(t)>h(4),求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() (含端点)上运动,当点
(含端点)上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com