
(本题满分14分)如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,
BD交AC于点E,F是PC中点,G为EC中点.
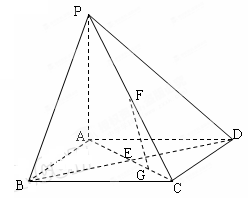
(1)求证:FG//平面PBD;
(2)当二面角B—PC—D的大小为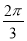 时,求FG与平面PCD所成角的正切值.
时,求FG与平面PCD所成角的正切值.
(1)详见解析;(2)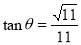 .
.
【解析】
试题分析:(1) 连接PE,G.、F为EC和PC的中点,由线面平行的判定定理,即可证明结果.(2)以AB为x轴,AD为y 轴,AP为z轴,建立如图空间直角坐标系,设AB=1,AP=t ,即可求出平面BPC的一个法向量为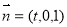 ,平面DPC的一个法向量为
,平面DPC的一个法向量为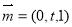 ,根据二面角B—PC—D的大小为
,根据二面角B—PC—D的大小为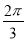 ,可得|
,可得|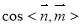 |=|
|=|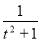 |=
|=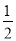 ,即可解得
,即可解得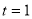 ,即可求出FG与平面PCD所成角
,即可求出FG与平面PCD所成角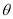 的正弦值.
的正弦值.
试题解析:(1) 连接PE,G.、F为EC和PC的中点,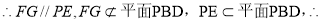 FG//平面PBD (5分)
FG//平面PBD (5分)
(2)以AB为x轴,AD为y 轴,AP为z轴,建立如图空间直角坐标系。
设AB=1,AP=t 则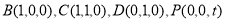 ,
,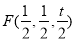 ,
, (7分)
(7分)
∴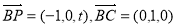 ∴平面BPC的一个法向量为
∴平面BPC的一个法向量为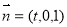
又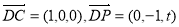 ∴平面DPC的一个法向量为
∴平面DPC的一个法向量为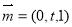 (9分)
(9分)
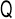 二面角B—PC—D的大小为
二面角B—PC—D的大小为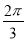 ,∴|
,∴|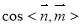 |=|
|=|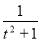 |=
|=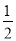
∴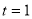 (11分)
(11分)
∴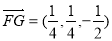 ∴FG与平面PCD所成角
∴FG与平面PCD所成角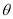 的正弦值
的正弦值 , (13分)
, (13分)
∴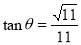 (14分)
(14分)
考点:1.线面平行的判断;2.二面角的应用.


科目:高中数学 来源:2014-2015学年内蒙古霍林郭勒市高一上学期期中考试数学试卷(解析版) 题型:选择题
集合{1,2,3}的非空子集共有( )
A 、5个 B、6个 C、 7个 D、 8个
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省金华市高三上学期期中考试文科数学试卷(解析版) 题型:选择题
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( )

 A.90° B.30° C.45° D.60°
A.90° B.30° C.45° D.60°
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省金华市高三上学期期中考试理科数学试卷(解析版) 题型:填空题
已知一个正三棱锥的正视图为等腰直角三形,其尺寸如图所示,则其侧视图的周长为 .
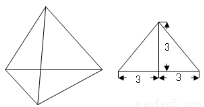
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省金华市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
若非零向量a,b满足︱a-b︱=︱b︱,则 ( )
A.︱2a︱<︱a-2b︱
B.︱2b︱<︱a-2b︱
C.︱2a︱>︱a-2b︱
D.︱2b︱>︱a-2b︱
查看答案和解析>>
科目:高中数学 来源:2014-2015学年宁夏银川市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,则输出的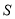 的值为( )
的值为( )
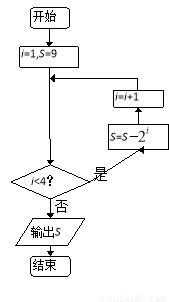
A. -7 B. 8 C. -9 D. -5
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试文科数学试卷(解析版) 题型:选择题
在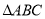 中,若
中,若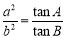 ,则
,则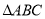 为( )
为( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com