
| 组别 | 分组(件数) | 频数 | 频率 |
| 一 | [50,60) | 1 | |
| 二 | [60,70) | c | |
| 三 | [70,80) | 10 | |
| 四 | [80,90) | b | 0.36 |
| 五 | [90,100) | 12 | |
| 六 | [100,110] | 6 | 0.12 |
| 合计 | a |
| 频数 |
| 样本容量 |
| 6 |
| a |
| 3 |
| 50 |
| 11 |
| 18 |
| 18 |
| 36 |
| 12 |
| 36 |
| 6 |
| 36 |
| 11 |
| 15 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
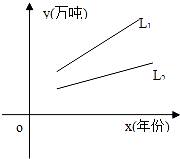 对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述:
对某种产品市场产销量情况如图所示,其中:L1表示产品各年年产量的变化规律;L2表示产品各年的销售情况.下列叙述:| A、(1)(2) |
| B、(2)(3) |
| C、(3)(4) |
| D、(1)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:
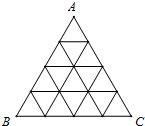 如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=
如图,将正△ABC分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A,B,C处的三个数互不相同且和为1,则所有顶点的数之和S=查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{3,5} | B、{3,7} |
| C、{3,5,7} | D、∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 13 |
| sinB |
| sinAsinC |
| BA |
| BC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com