
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 由题意可得求函数y=f(|x|)的图象和直线y=a的交点个数.作出函数y=f(|x|)的图象,平移直线y=a,即可得到所求交点个数,进而得到结论
解答  解:函数f(x)=$\left\{\begin{array}{l}{log_2}(1-x),x<1\\-{(x-2)^2}+2,x≥1\end{array}$,方程f(|x|)=a,(a∈R)实根个数,
解:函数f(x)=$\left\{\begin{array}{l}{log_2}(1-x),x<1\\-{(x-2)^2}+2,x≥1\end{array}$,方程f(|x|)=a,(a∈R)实根个数,
即为函数y=f(|x|)和直线y=a的交点个数.
由y=f(|x|)为偶函数,可得图象关于y轴对称.
作出函数y=f(|x|)的图象,如图,
平移直线y=a,可得它们有2个、3个、4个交点.
不可能有5个交点,即不可能有5个实根,
故选:A.
点评 本题考查方程的实根个数问题的解法,注意运用转化思想和数形结合的方法,考查判断和作图能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
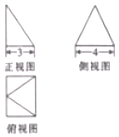 某几何体的三视图如图所示,其侧视图是一个等边三角形,则此几何体的体积是( )
某几何体的三视图如图所示,其侧视图是一个等边三角形,则此几何体的体积是( )| A. | 24$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 16$\sqrt{3}$ | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com