
分析 (Ⅰ)讨论f(x)的单调性,很容易想到求导数的办法,通过导函数f′(x)的符号判断单调性,注意到导函数中二次函数的部分,判别式的值以及m的符号判断即可.
(Ⅱ)g(x)=f(x)-$\frac{2}{m}$x-5恰有两个零点,转化为方程有两个解,转化为两个函数有两个交点.判断直线经过的顶点,通过f(x)的导数,曲线的斜率,推出m 的范围.
解答 解:(Ⅰ)f(x)=(x2-$\frac{3}{m}$x+$\frac{5}{{m}^{2}}$)emx,其中实数m≠0.
可得f′(x)=(mx2-x+$\frac{2}{m}$)emx,其中实数m≠0.∵emx>0,∴f′(x)的符号,只与mx2-x+$\frac{2}{m}$的符号有关.
令y=mx2-x+$\frac{2}{m}$,m≠0,△=1-4m$•\frac{2}{m}$=-7<0.
当m>0时,y>0恒成立,此时f′(x)>0,恒成立.函数在R上是增函数.
当m<0时,y<0恒成立,此时f′(x)<0,恒成立.函数在R上是减函数.
(Ⅱ)g(x)=f(x)-$\frac{2}{m}$x-5恰有两个零点,即f(x)=$\frac{2}{m}$x+5恰有两个解,
也就是f(x)=(x2-$\frac{3}{m}$x+$\frac{5}{{m}^{2}}$)emx,与g(x)=$\frac{2}{m}$x+5有两个交点.
因为g(x)=$\frac{2}{m}$x+5恒过(0,5),当m=1时,f(x)=(x2-3x+5)ex,经过(0,5),并且f′(x)=(x2-x+2)ex,此时f′(0)=2,g(x)=2x+5的斜率也为2,如图: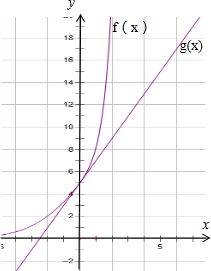
当m>1时.两个函数有两个交点.
当m∈(0,1)时,f(x)经过(0,$\frac{5}{{m}^{2}}$),$\frac{5}{{m}^{2}}>5$,此时两个函数至多有一个交点.
当m<0时,两个函数都是减函数,m=-1时,两个函数的图象如图:
m<-1时,两个函数有两个交点.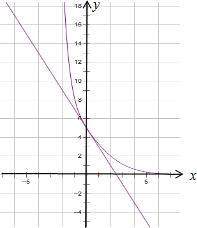
综上,m<-1或m>1.
点评 本题考查函数的导数的综合应用,函数的单调性以及函数的零点的个数,考查转化思想以及数形结合思想的应用,难度比较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
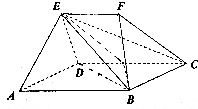 如图所示,在多面体ABCDEF中,面ABCD是平行四边形,EF∥AB,EF:AB=1:2,则四棱锥E-ABCD与三棱锥E-BCF的体积比为4.
如图所示,在多面体ABCDEF中,面ABCD是平行四边形,EF∥AB,EF:AB=1:2,则四棱锥E-ABCD与三棱锥E-BCF的体积比为4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com