
分析 (1)由x>0,y>0,2n-nx>0,可求得x=1,则Dn内的整点在直线x=1上,联立可求得整点纵坐标,进而可得整点个数;
(2)求得bn=${2^{a_n}}$+(-1)nan=2n+(-1)nn,运用数列的求和方法:分组求和,结合等比数列的求和公式,计算即可得到所求和.
解答 解:(1)由x>0,y>0,2n-nx>0,得0<x<2,x为整数,∴x=1,
∴Dn内的整点在直线x=1上,记直线y=-nx+2n为l,
l与直线x=1的交点的纵坐标分别为y1,
则y1=-n+2n=n,
∴an=n(n∈N*);
(2)bn=${2^{a_n}}$+(-1)nan=2n+(-1)nn,
则数列{bn}的前2n项和T2n=(2+22+…+22n)+[-1+2-3+4-…-(2n-1)+2n]
=$\frac{2(1-{2}^{2n})}{1-2}$+n=22n+1-2+n.
点评 本题考查数列与不等式的综合,考查线性规划的基本知识,等比数列的求和公式,考查学生分析解决问题的能力,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
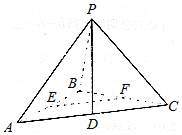 如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.
如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 6 | C. | $2\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com