
 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=3上,圆弧C1的圆心是坐标原点O,半径为5,圆弧C2过点A(-1,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=3上,圆弧C1的圆心是坐标原点O,半径为5,圆弧C2过点A(-1,0).分析 (1)由圆弧C1所在圆的方程求出M、N的坐标,求出直线AM的中垂线方程与直线MN中垂线方程,再求出圆弧C2所在圆的圆心和半径,即可求出圆弧C2所在圆的方程;
(2)先假设存在这样的点P(x,y),根据条件和两点的距离公式列出方程化简,求出点P的轨迹方程,分别与圆弧C1的方程、圆弧C2的方程联立后求出P的坐标即可得到答案.
解答 解:(1)圆弧C1所在圆的方程为x2+y2=25,
令x=3,解得M(3,4),N(3,-4),
∵圆弧C2过点A(-1,0),
∴直线AM的中垂线方程为y-2=-(x-1),
∵直线MN的中垂线方程y=0上,
∴令y=0,得圆弧C2所在圆的圆心为O2(3,0),
∴圆弧C2所在圆的半径为r2=|O2A|=4,
∴圆弧C2的方程为(x-3)2+y2=16(-1≤x≤3);(6分)
(2)假设存在这样的点P(x,y),
由$PA=\frac{{\sqrt{2}}}{2}PO$得,$\sqrt{(x+1)^{2}+{y}^{2}}=\frac{\sqrt{2}}{2}\sqrt{{x}^{2}+{y}^{2}}$,
化简得,x2+y2+4x+2=0,(8分)
∴点P的轨迹方程是x2+y2+4x+2=0,
由$\left\{{\begin{array}{l}{{x^2}+{y^2}+4x+2=0}\\{{x^2}+{y^2}=25(-5≤x≤3)}\end{array}}\right.$,
解得$x=-\frac{27}{4}$(舍去),
由$\left\{{\begin{array}{l}{{x^2}+{y^2}+4x+2=0}\\{{{(x-3)}^2}+{y^2}=16(-1≤x≤3)}\end{array}}\right.$,
解得$x=-\frac{9}{10},y=±\frac{{\sqrt{79}}}{10}$,
综上知的,这样的点P存在2个.(12分)
点评 本题考查直线与圆的位置关系,圆的方程求法:几何法,以及两点间的距离公式,考查了方程思想,化简、计算能力,属于中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [-18,6] | B. | [6-5$\sqrt{2}$,6+5$\sqrt{2}$] | C. | [-16,4] | D. | [-6-5$\sqrt{2}$,-6+5$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | $\frac{32\sqrt{3}π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{64\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
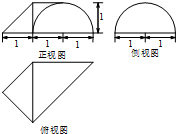
| A. | $\frac{π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| P(K2>k0) | 0.10 | 0.05 | 0.01 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com