
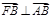 时,其离心率为
时,其离心率为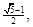 此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( )
此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( ) 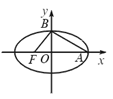
A.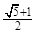 | B.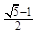 | C.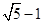 | D.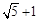 |
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源:不详 题型:解答题

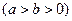 的离心率为
的离心率为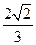 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为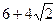 .
.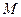 的方程;
的方程;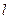 与椭圆
与椭圆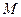 交于
交于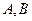 两点,且以
两点,且以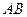 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点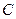 ,
, 面积的最大值.
面积的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
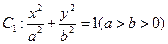 的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线
的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线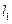 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线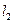 垂直
垂直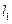 于点
于点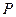 ,线段
,线段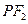 垂直平分线交
垂直平分线交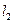 于点
于点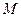
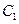 的标准方程和动点
的标准方程和动点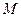 的轨迹
的轨迹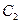 的方程。
的方程。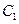 的右焦点
的右焦点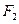 作斜率为1的直线交椭圆于A、B两点,求
作斜率为1的直线交椭圆于A、B两点,求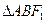 的面积。
的面积。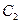 与
与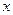 轴交于点
轴交于点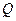 ,不同的两点
,不同的两点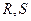 在轨迹
在轨迹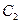 上,
上,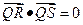 求证:直线
求证:直线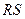 恒过
恒过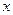 轴上的定点。
轴上的定点。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
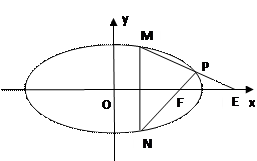
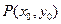 、
、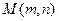 是圆锥曲线C上不与顶点重合的任意两点,
是圆锥曲线C上不与顶点重合的任意两点, 是垂直于
是垂直于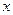 轴的一条垂轴弦,直线
轴的一条垂轴弦,直线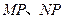 分别交
分别交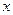 轴于点
轴于点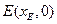 和点
和点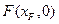 。
。
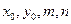 的代数式分别表示
的代数式分别表示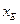
 和
和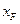 ;
;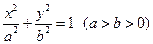 (如图),求证:
(如图),求证: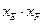 是与
是与 和点
和点 位置无关的定值;
位置无关的定值;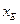 和
和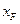 经过某种四则运算(加、减、乘、除),其结果是否是与
经过某种四则运算(加、减、乘、除),其结果是否是与 和点
和点 位置无关的定值,写出你的研究结论并证明。
位置无关的定值,写出你的研究结论并证明。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
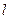 与中心在原点,焦点在x轴上且离心率为
与中心在原点,焦点在x轴上且离心率为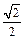 的椭圆C相
的椭圆C相 交于A、B两点,直线y=
交于A、B两点,直线y=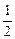 x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l
x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l 对称,试求直线l与椭圆C的方程
对称,试求直线l与椭圆C的方程
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com