
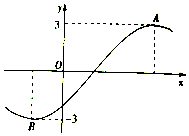
 已知函数f(x)=3sin(ωx+ϕ)$(ω>0,|ϕ|≤\frac{π}{2})$的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )
已知函数f(x)=3sin(ωx+ϕ)$(ω>0,|ϕ|≤\frac{π}{2})$的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据图象求出A,ω 和φ,即可求函数f(x)的解析式;在平移变换函数图象关于y轴对称求解t的关系式.
解答 解:由题设图象知,周期$\frac{1}{2}$T=|AB|,解得:T=20,
∴ω=$\frac{2π}{T}$=$\frac{π}{10}$.
可得f(x)=3sin($\frac{π}{10}x$+ϕ)
∵f(2)=0,
∴sin($\frac{π}{10}×2$+ϕ)=0,
∵$-\frac{π}{2}≤$Φ$≤\frac{π}{2}$,
∴ϕ=$-\frac{π}{5}$.
故得f(x)=3sin($\frac{π}{10}x$-$\frac{π}{5}$)
将函数f(x)的图象向右平移t(t>0)的单位可得:y=3sin[$\frac{π}{10}(x-t)$)$-\frac{π}{5}$]=3in($\frac{π}{10}x-\frac{π}{10}t-\frac{π}{5}$),
函数图象关于y轴对称,
∴$-\frac{π}{10}t-\frac{π}{5}=\frac{π}{2}+kπ$,
整理得:-t=7+10k,
∵t>0,
∴当k=-1时,t的最小值为3.
故选C
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
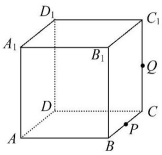 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②④(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②④(写出所有正确命题的编号).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}\sqrt{3}$ | B. | 3 | C. | $\frac{4}{3}\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 84 | B. | 78 | C. | 81 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x<2} | B. | {x|-1≤x<2} | C. | {x|-1<x≤1} | D. | {x|0<x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “m∥α,m∥β”是“α∥β”的充分不必要条件 | |
| B. | m∥n时,“m∥β”是“n∥β”的必要不充分条件 | |
| C. | n?α时,“m⊥α”是“m⊥n”的既不充分也不必要条件 | |
| D. | m⊥α,n⊥β时,“m⊥n”是“α⊥β”的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com