
分析 根据体积,建立方程组,求出M的坐标,可得直线OM的斜率,利用基本不等式可得结论.
解答 解:设P(2pt,2pt),M(x,y),则$\left\{\begin{array}{l}{x-\frac{p}{2}=\frac{2p}{3}{t}^{2}-\frac{p}{6}}\\{y=\frac{2pt}{3}}\end{array}\right.$,
∴x=$\frac{2p}{3}{t}^{2}+\frac{p}{3}$,y=$\frac{2pt}{3}$,
∴kOM=$\frac{2t}{2{t}^{2}+1}$=$\frac{1}{t+\frac{1}{2t}}$≤$\frac{1}{2\sqrt{\frac{1}{2}}}$=$\frac{\sqrt{2}}{2}$,
当且仅当t=$\frac{1}{2t}$时取等号,
∴直线OM的斜率的最大值为$\frac{{\sqrt{2}}}{2}$.
故答案为:$\frac{{\sqrt{2}}}{2}$.
点评 本题考查抛物线的方程及运用,考查直线的斜率的最大值,考查基本不等式,考查运算能力,属于中档题.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
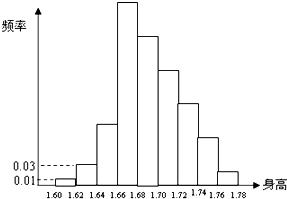 为了解某校身高在1.60m~1.78m的高一学生的情况,随机地抽查了该校200名高一学生,得到如图1所示频率直方图.由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为m,身高在1.66m~1.74m的学生数为n,则m,n的值分别为( )
为了解某校身高在1.60m~1.78m的高一学生的情况,随机地抽查了该校200名高一学生,得到如图1所示频率直方图.由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为m,身高在1.66m~1.74m的学生数为n,则m,n的值分别为( )| A. | 0.27,78 | B. | 0.27,156 | C. | 0.81,78 | D. | 0.09,83 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=4-2x | B. | f(x)=$\frac{1}{x-2}$ | C. | f(x)=x2-2x-2 | D. | f(x)=-|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com