
分析 (1)由${l_1}:y=\sqrt{3}x+2\sqrt{3}$与${l_2}:y=-\sqrt{3}x$联立可得交点坐标,利用互化公式可得P点的极坐标.
(2)设以原点为极点,x轴正半轴为极轴建立极坐标系,把x=ρcosθ,y=ρsinθ代入椭圆方程有$\frac{1}{ρ^2}=\frac{{{{cos}^2}θ}}{4}+{sin^2}θ$,不妨取A(ρ1,θ),B(ρ2,θ+120°)C(ρ3,θ-120°),代入利用和差公式、三角函数基本关系式即可得出.
解答 解:(1)由${l_1}:y=\sqrt{3}x+2\sqrt{3}$与${l_2}:y=-\sqrt{3}x$联立,可得交点坐标为$P(-1,\sqrt{3})$,化为P点的极坐标为$P(2,\frac{2π}{3})$.
(2)设以原点为极点,x轴正半轴为极轴建立极坐标系,把x=ρcosθ,y=ρsinθ代入椭圆方程有$\frac{1}{ρ^2}=\frac{{{{cos}^2}θ}}{4}+{sin^2}θ$,不妨取A(ρ1,θ),B(ρ2,θ+120°)C(ρ3,θ-120°),
则$\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OB}|}^2}}}+\frac{1}{{{{|{OC}|}^2}}}$=$\frac{1}{ρ_1^2}$+$\frac{1}{ρ_2^2}$+$\frac{1}{ρ_3^2}$=$\frac{1}{4}[{cos^2}θ+{cos^2}(θ+{120°})+{cos^2}(θ-{120°})]$+[sin2θ+sin2(θ+120°)+sin2(θ-120°)]
=$\frac{1}{4}[{cos^2}θ+\frac{1}{4}{(cosθ+\sqrt{3}sinθ)^2}+\frac{1}{4}{(cosθ-\sqrt{3}sinθ)^2}]$$+{sin^2}θ+\frac{1}{4}{(-sinθ+\sqrt{3}cosθ)^2}+\frac{1}{4}{(sinθ+\sqrt{3}cosθ)^2}]$
=$\frac{15}{8}$.
点评 本题考查了极坐标与直角坐标互化公式、直线的交点、和差公式、三角函数基本关系式,考查了推理能力,属于中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}sin2θ$ | B. | $-\frac{1}{2}sin2θ$ | C. | sin2θ | D. | -sin2θ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
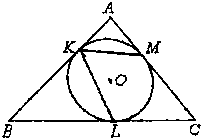 如图,已知在△ABC中有内切圆⊙O,分别切三边于K、L、M,⊙O的面积为27π,∠MKL=60°,BC:AC=8:5.求:
如图,已知在△ABC中有内切圆⊙O,分别切三边于K、L、M,⊙O的面积为27π,∠MKL=60°,BC:AC=8:5.求:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<0} | B. | {x|2<x<3} | C. | {x|2≤x<3} | D. | {x|x≤-2或2≤x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com