Question

13．已知直线l：y=k（x+1）-$\sqrt{3}$与圆x²+y²=（2$\sqrt{3}$）²交于A、B两点，过A、B分别作l的垂线与x轴交于C、D两点，若|AB|=4$\sqrt{3}$，则|CD|=$8\sqrt{3}$．

Answer 1

分析 根据直线与圆相交，圆x²+y²=（2$\sqrt{3}$）²可知：圆心为（0，0），半径r=2$\sqrt{3}$，弦长为|AB|=4$\sqrt{3}$=2r，说明直线过圆心．求解k的值．得到直线AB的倾斜角，根据AOC和OBD是两个全等的直角三角形，OA=OB=2$\sqrt{3}$
即可求出OC和OD．即可得到|CD|的长度．

解答 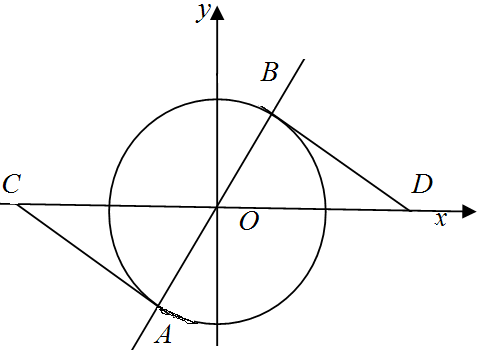解：由圆的方程x²+y²=（2$\sqrt{3}$）²可知：圆心为（0，0），半径r=2$\sqrt{3}$，
∵弦长为|AB|=4$\sqrt{3}$=2r，说明，直线过圆心．
则有：0=k（0-1）-$\sqrt{3}$，解得k=$\sqrt{3}$，
直线AB的方程为：y=$\sqrt{3}$x．
设直线AB的倾斜角为θ，则tanθ=$\sqrt{3}$，
∴θ=60°
Rt△AOC中：|CO|=$\frac{|OA|}{cos60°}$=$\frac{2\sqrt{3}}{\frac{1}{2}}$=$4\sqrt{3}$
那么：|CD|=2|OC|=$8\sqrt{3}$
故答案为：$8\sqrt{3}$．

点评 本题考查了直线与圆的位置关系的运用，弦长的问题．属于基础题．