
分析 把解析式配方得出f(1$+\frac{1}{x}$)=($\frac{1}{x}$+1)2-($\frac{1}{x}$+1)+1,整体换元即可求解.
解答 解:∵f(1+$\frac{1}{x}$)=$\frac{1}{x}$+$\frac{{x}^{2}+1}{{x}^{2}}$,
∴f(1$+\frac{1}{x}$)=($\frac{1}{x}$+1)2-($\frac{1}{x}$+1)+1,
设t=1$+\frac{1}{x}$,f(t)=t2-t+1,
∵1$+\frac{1}{x}$≠1
∴f(x)=x2-x+1,x≠1.
点评 本题考察了运用配方法,换元法求解函数的解析式,关键是注意变量的范围限制,属于中档题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
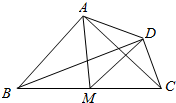 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com