Question

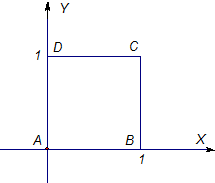
9．如图，在直角坐标系中，正方形ABCD的四个顶点分别为A（0，0），B（1，0），C（1，1），D（0，1）．
（Ⅰ）已知函数$f（x）=\frac{2}{9x}$（其中$x∈（\frac{1}{3}，\frac{2}{3}）$），过f（x）图象是任意一点R的切线l将正方形ABCD截成两部分，设R点的横坐标为t，S（t）表示正方形ABCD被切线l所截的左下部分的面积，求S（t）的解析式；
（Ⅱ） 试问S（t）在定义域上是否存在最大值和最小值？若存在，求出S（t）的最大值和最小值；若不存在，请说明理由．

Answer 1

分析 （Ⅰ）讨论切点位置，得到不同的切点位置对应的面积解析式；注意讨论要全面；
（Ⅱ）由（Ⅰ）的解析式分析各段的单调性，全等最值．

解答 解：（Ⅰ）设R（t，f（t））（其中$t∈（\frac{1}{3}，\frac{2}{3}）$），f（x）图象上的两端点为$E（\frac{1}{3}，\frac{2}{3}），F（\frac{2}{3}，\frac{1}{3}）$
又$f'（t）=-\frac{2}{{9{t^2}}}$，
所以过点R（t，f（t））的切线l的方程为：$y=-\frac{2}{{9{t^2}}}x+\frac{4}{9t}$…（2分）
（ⅰ）当切点为$E（\frac{1}{3}，\frac{2}{3}）$时，$t=\frac{1}{3}$，切线l为：$y=-2x+\frac{4}{3}$，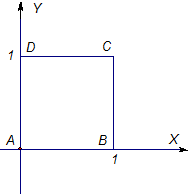

切线l与CD的交点坐标为$（\frac{1}{6}，1）$．当切线过点D（0，1）时，$t=\frac{4}{9}$…（4分）
故当$\frac{1}{3}＜t＜\frac{4}{9}$时，切线l与CD相交，此时正方形ABCD被切线l所截的左下部分是直角梯形，S（t）=$\frac{1}{2}[\frac{（4-9t）t}{2}+2t]=\frac{1}{4}（-9{t^2}+8t）$…（6分）
（ⅱ）当切线过点B（1，0）时，当$\frac{4}{9}≤t≤\frac{1}{2}$时，切线l与AD，AB都相交，正方形ABCD被切线l所截的左下部分是直角三角形，S（t）=$\frac{1}{2}（\frac{4}{9t}）（2t）=\frac{4}{9}$…（7分）
（ⅲ）当切点为$F（\frac{2}{3}，\frac{1}{3}）$时，切线l为：$y=-\frac{1}{2}x+\frac{2}{3}$，切线l与BC的交点坐标为$（1，\frac{1}{6}）$
故当$\frac{1}{2}＜t＜\frac{2}{3}$时，切线l与AD，BC都相交，正方形ABCD被切线l所截的左下部分是直角梯形，S（t）=$\frac{1}{2}（\frac{4}{9t}+\frac{4t-2}{{9{t^2}}}]=\frac{4}{9t}-\frac{1}{{9{t^2}}}$…（9分）
综上所述：$S（t）=\left\{{\begin{array}{l}{\frac{1}{4}（-9{t^2}+8t）t∈（\frac{1}{3}，\frac{4}{9}）}\\{\frac{4}{9}\;\;\;t∈[\frac{4}{9}，\frac{1}{2}]}\\{\frac{4}{9t}-\frac{1}{{9{t^2}}}\;t∈（\frac{1}{2}，\frac{2}{3}）}\end{array}}\right.$…（10分）
（Ⅱ）解：当$t∈（\frac{1}{3}，\frac{4}{9}）$，$S'（t）=-\frac{9}{2}（t-\frac{4}{9}）＞0$，故S（t）在$（\frac{1}{3}，\frac{4}{9}）$上递增，S（t）最大无限接近$\frac{4}{9}$，S（t）无最大值和最小值…（11分）
当$t∈（\frac{1}{2}，\frac{2}{3}）$时，$S'（t）=\frac{2（1-2t）}{{9{t^3}}}＜0$，S（t）在$（\frac{1}{2}，\frac{2}{3}）$上递减，S（t）最大无限接近$\frac{4}{9}$，S（t）无最大值和最小值…（12分）
故当$t∈[\frac{4}{9}，\frac{1}{2}]$，$S（t）=\frac{4}{9}$成立…（13分）
综上所述：S（t）在定义域上存在最大值$\frac{4}{9}$，不存在最小值．…（14分）．

点评 本题考查了分段函数进行是求法与函数的最值求法；借助于导数的几何意义、利用单调性求最值；考查了学生的计算能力；属于难题．