
分析 (Ⅰ)根据函数的定义即可得到结论.
(Ⅱ)根据函数单调性的定义进行判断证明即可;
(Ⅲ)根据三角函数的关系进行解方程即可.
解答 解:(Ⅰ)∵f(x)的定义域为(-∞,1)∪(1,+∞),g(x)的定义域为R,
∴$h(x)=\left\{\begin{array}{l}\frac{x^2}{x-1},x∈(-∞,1)∪(1,+∞)\\ 1,x=1\end{array}\right.$
(Ⅱ)当x>1时,$h(x)=\frac{x^2}{x-1}$
任意取x1<x2∈(1,+∞),则$h({x_1})-h({x_2})=\frac{{{x_1}^2}}{{{x_1}-1}}-\frac{{{x_2}^2}}{{{x_2}-1}}=\frac{{({x_1}-{x_2})[{x_1}{x_2}-({x_1}+{x_2})]}}{{({x_1}-1)({x_2}-1)}}$,
∵${x_1}<{x_2}∈(1,+∞)\begin{array}{l}{\;}&{∴{x_1}-{x_2}<0,{x_1}-1>0,{x_2}-1>0}\end{array}$
①当x1<x2∈(1,2)时,x1x2-(x1+x2)<0,即h(x1)-h(x2)>0,
∴h(x1)>h(x2),故,h(x)在(1,2)上单调递减.
②当x1<x2∈(2,+∞)时,x1x2-(x1+x2)>0,即h(x1)-h(x2)<0,
∴h(x1)<h(x2),故,h(x)在(2,+∞)上单调递增.
综上,h(x)在(1,2)上单调递减,h(x)在(2,+∞)上单调递增.
(Ⅲ)由函数y=f(x)的定义域为R,得g(x)=f(x+α)的定义域为R,
∴对于任意x∈R,都有h(x)=f(x)g(x)
即对于任意x∈R,都有cos4x=f(x)f(x+α),
∴我们考虑将cos4x分解成两个函数的乘积,
而且这两个函数还可以通过平移相互转化cos4x=cos22x-sin22x=(cos2x+sin2x)(cos2x-sin2x)=$\sqrt{2}cos(2x-\frac{π}{4})•\sqrt{2}cos(2x+\frac{π}{4})$,
∴可取$f(x)=\sqrt{2}cos(2x-\frac{π}{4})$,$α=\frac{π}{4}$即可.
(答案不唯一)
点评 本题主要考查函数单调性的应用,根据函数单调性的定义是解决本题的关键.综合考查函数的性质.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
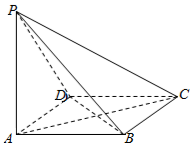 如图,四棱锥P-ABCD的底面为菱形,且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面为菱形,且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=$\sqrt{3}$. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0∉N | B. | $0•\overrightarrow{AB}=0$ | C. | cos0.75°>cos0.7 | D. | lge>(lge)2>lg$\sqrt{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥1} | B. | {x|x>1} | C. | {x|0<x<1} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com