
分析 (Ⅰ)再写一式,两式相减,即可证明数列{an+1}是等比数列,并求数列{an}的通项公式;
(Ⅱ)bn=an+2n+1=3n+2n,可得$\frac{1}{{3}^{n}+{2}^{n}}$<$\frac{1}{{2}^{n+1}}$,即可证明结论.
解答 解:(Ⅰ)由2Sn=3an-2n得:2Sn-1=3an-1-2(n-1),
∴2Sn-2Sn-1=3an-3an-1-2,即:an=3an-1+2
∴an+1=3(an-1+1),所以{an+1}是以a1+1为首项,公比为3的等比数列,
由2S1=3a1-2知a1=2,
∴an+1=3n,即an=3n-1;
(Ⅱ)证明:bn=an+2n+1=3n+2n,
∵3n+2n>2n+2n=2n+1,
∴$\frac{1}{{3}^{n}+{2}^{n}}$<$\frac{1}{{2}^{n+1}}$,
∴$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$=$\frac{1}{3+2}$+$\frac{1}{{3}^{2}+{2}^{2}}$+…+$\frac{1}{{3}^{n}+{2}^{n}}$<$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$…+$\frac{1}{{2}^{n+1}}$=$\frac{1}{2}-\frac{1}{{2}^{n+1}}$.
点评 本题考查等比数列的证明,考查数列与不等式的综合,考查放缩方法的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [1,3] | C. | [-1,3] | D. | (-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
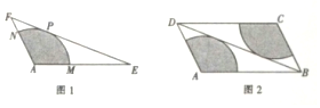
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
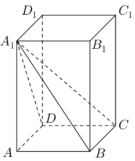 如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3;
如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
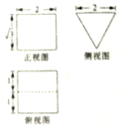
| A. | 20π | B. | $\frac{44}{3}$π | C. | $\frac{28}{3}$π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在$(0,\frac{π}{2})$单调递减 | B. | f(x)在$(\frac{π}{4},\frac{3π}{4})$单调递减 | ||
| C. | f(x)在$(0,\frac{π}{2})$单调递增 | D. | f(x)在$(\frac{π}{4},\frac{3π}{4})$单调递增 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com