练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$，$\overrightarrow{{e}_{3}}$是不共面的三个向量，则λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$是λ2+μ2+v2=0的（　　）
    A．充分但不必要条件B．必要但不充分条件
    C．充要条件D．既不充分又不必要条件

    分析 $\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$，$\overrightarrow{{e}_{3}}$是不共面的三个向量，则λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$?λ=μ=v?λ2+μ2+v2=0，即可判断出结论．

    解答 解：∵$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$，$\overrightarrow{{e}_{3}}$是不共面的三个向量，则λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$?λ=μ=v?λ2+μ2+v2=0，
    ∴λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$是λ2+μ2+v2=0的充要条件，
    故选：C．

    点评 本题考查了空间向量基本定理、简易逻辑的判定，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

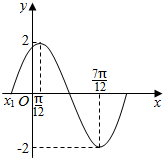    16．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）在一个周期内的图象如图所示．
    （]）求f（x）其解析式；
    （2）求f（x）的对称中心；
    （3）方程f（x）-m=0在x∈[0，$\frac{π}{2}$]上有两个解，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知x，y∈R，且满足$\left\{\begin{array}{l}{x≥1}\\{y≥x}\\{x-2y+3≥0}\end{array}\right.$，则t=$\frac{y+1}{x}$的最大值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．求函数f（x）=3sin2x+8cos2x-4，x∈[0，$\frac{π}{2}$]的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知$\frac{π}{4}$＜β＜α＜$\frac{3π}{4}$，且cos（α-β）=$\frac{12}{13}$，sin（α+β）=-$\frac{3}{5}$，求sin2α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．如图，矩形ABCD中AD边的长为1，AB边的长为2，矩形ABCD位于第一象限，且顶点A，D分别在x轴y轴的正半轴上（含原点）滑动，则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是（　　）
    A．$\sqrt{5}$B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知O为△ABC所在平面内一点，且$\overrightarrow{OA}$2+$\overrightarrow{BC}$2=$\overrightarrow{OB}$2+$\overrightarrow{CA}$2=$\overrightarrow{OC}$2+$\overrightarrow{AB}$2，则O一定为△ABC的垂心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设函数$f（x）={2^{\sqrt{-{x^2}+2x+\frac{5}{4}}}}$，对于给定的正数K，定义函数fg（x）=$\left\{{\begin{array}{l}{f（x），f（x）≥K}\\{K，f（x）＜K}\end{array}}$，若对于函数$f（x）={2^{\sqrt{-{x^2}+2x+\frac{5}{4}}}}$定义域内的任意x，恒有fg（x）=f（x），则（　　）
    A．K的最小值为1B．K的最大值为1C．K的最小值为$2\sqrt{2}$D．K的最大值为$2\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若一段圆弧的长度等于该圆内接正三角形的边长，则这段弧所对圆心角弧度为（　　）
    A．$\frac{π}{3}$B．$\frac{2π}{3}$C．$\sqrt{3}$D．$\sqrt{2}$

    查看答案和解析>>

    同步练习册答案