
分析 由题意和辅助角公式可得f(x)=5sin(2x+φ),φ=arctan$\frac{4}{3}$,由x∈[0,$\frac{π}{2}$]可得2x+φ∈[arctan$\frac{4}{3}$,π+arctan$\frac{4}{3}$],由正弦函数值域可得.
解答 解:由三角函数公式化简可得f(x)=3sin2x+8cos2x-4
=3sin2x+4(2cos2x-1)=3sin2x+4cos2x=5sin(2x+φ),
其中tanφ=$\frac{4}{3}$,故φ=arctan$\frac{4}{3}$,
∵x∈[0,$\frac{π}{2}$],∴2x∈[0,π],∴2x+φ∈[arctan$\frac{4}{3}$,π+arctan$\frac{4}{3}$],
∴当2x+φ=$\frac{π}{2}$时,f(x)=5sin(2x+φ)取最大值5;
当2x+φ=π+arctan$\frac{4}{3}$时,f(x)=5sin(2x+φ)取最小值5×(-$\frac{4}{5}$)=-4.
故函数的值域为[-4,5].
点评 本题考查三角函数求最值,涉及辅助角公式和同角三角函数基本关系,属中档题.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
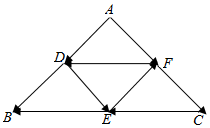 如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.
如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{11}{14}$ | B. | $\frac{12}{7}$ | C. | -$\frac{11}{24}$ | D. | -$\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-1} | B. | {x|x≠2} | C. | [-1,2)∪(2,+∞) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com