
分析 ①可先根据三角形内角和定理判断角α的范围,从而确定cosα的值域;
②构造函数f(x)=$\frac{sinx}{x}$(0<x<π),应用导数求单调性,从而得到B<A,即可判断②;
③将$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,化简整理运用不共线结论,得到2a=b=c,再运用余弦定理求出cosA,即可判断;
④构造函数f(x)=tsinx-sin(tx),应用导数运用单调性得到tsinB<sin(tB),又sinA<tsinB,再根据和差化积公式,结合角的范围即可判断.
解答 解:①假设三个内角都小于60°,则三内角和必小于180°,与内角和定理矛盾,故必有一内角大于或等于60°,设为α,则cosα≤cos60°=$\frac{1}{2}$,故①正确;
②设函数f(x)=$\frac{sinx}{x}$(0<x<π),则导数f′(x)=$\frac{xcosx-sinx}{{x}^{2}}$,
若$\frac{π}{2}$≤x<π,则f′(x)<0,
又AsinB>BsinA,即 $\frac{sinB}{B}$>$\frac{sinA}{A}$⇒B<A,
若0<x<$\frac{π}{2}$,则由于tanx>x,
故f′(x)<0,即有B<A,故②正确;
③若2a$\overrightarrow{BC}$+b$\overrightarrow{CA}$+c$\overrightarrow{AB}$=$\overrightarrow{0}$,即2a( $\overrightarrow{AC}-\overrightarrow{AB}$)-b $\overrightarrow{AC}$+c $\overrightarrow{AB}$=$\overrightarrow{0}$,即(2a-b) $\overrightarrow{AC}$=(2a-c) $\overrightarrow{AB}$,
由于 $\overrightarrow{AC}$,$\overrightarrow{AB}$不共线,故2a-b=2a-c=0,即2a=b=c,
由余弦定理得,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{7}{8}$>$\frac{\sqrt{3}}{2}$,
故最小角小于$\frac{π}{6}$,故③正确;
④若a<tb(0<t≤1),则由正弦定理得,sinA<tsinB,
令f(x)=tsinx-sin(tx),则f′(x)=tcosx-tcos(tx),
由于0<tx<x<π,则cos(tx)>cosx,即f′(x)<0,tsinx<sin(tx)即tsinB<sin(tB),
故有sinA<sin(tB),即2cos $\frac{A+tB}{2}$sin $\frac{A-tB}{2}$<0,
故有A<tB,故⑤正确.
故答案为:①②③④.
点评 本题以命题的真假判断为载体,考查正弦、余弦定理及应用,考查向量中这样一个结论:若a $\overrightarrow{OA}$+b$\overrightarrow{OB}$=$\overrightarrow{0}$($\overrightarrow{OA}$,$\overrightarrow{OB}$不共线)则a=b=0,还考查三角形中的边角关系以及构造函数应用单调性证明结论,属于综合题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
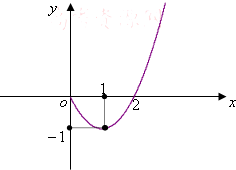 已知二次函数y=f(x)在[0,+∞)上的图象如图所示,顶点坐标为(1,-1).
已知二次函数y=f(x)在[0,+∞)上的图象如图所示,顶点坐标为(1,-1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
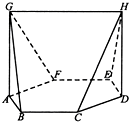 如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且
如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com