
分析 (Ⅰ)由代入法,计算数列的前4项,猜想an=$\frac{1}{n}$(n∈N*),可由数学归纳法证明;
(Ⅱ)由anan+1=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,运用裂项相消求和,即可得到所求和.
解答 解:(Ⅰ)∵a1=1,∴${a_2}=\frac{a_1}{{1+{a_1}}}=\frac{1}{2},{a_3}=\frac{a_2}{{1+{a_2}}}=\frac{1}{3},{a_4}=\frac{1}{4}$,
猜想${a_n}=\frac{1}{n},(n∈{N^*})$.
理由:当n=1时,a1=1显然成立;
设n=k(k∈N*)ak=$\frac{1}{k}$,
当n=k+1时,ak+1=$\frac{{a}_{k}}{1+{a}_{k}}$=$\frac{\frac{1}{k}}{1+\frac{1}{k}}$=$\frac{1}{1+k}$,
则n=k+1,猜想也成立.
则an=$\frac{1}{n}$(n∈N*);
(Ⅱ)S=a1a2+a2a3+a3a4+…+a7a8,
即有$S=\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{7×8}$=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{7}-\frac{1}{8})=1-\frac{1}{8}=\frac{7}{8}$.
点评 本题考查数列的通项公式,注意运用猜想和证明,考查数列的求和方法:裂项相消求和,考查运算能力,属于中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
| 分公司名称 | 雅雨 | 雅雨 | 雅女 | 雅竹 | 雅茶 |
| 月销售额x(万元) | 3 | 5 | 6 | 7 | 9 |
| 月利润y(万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组| A. | 32 | B. | 40 | C. | 48 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{c}{a}>\frac{d}{b}$ | B. | $\frac{c}{a}<\frac{d}{b}$ | C. | $\frac{c}{b}>\frac{d}{a}$ | D. | $\frac{c}{b}<\frac{d}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
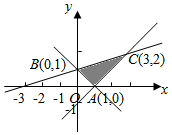 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )| A. | $\frac{1}{2}$ | B. | 0 | C. | $-\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 65 | B. | 75 | C. | 90 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com