练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设z1，z2是复数，则下列命题中的假命题是(　　)

    A．若|z1－z2|＝0，则＝

    B．若z1＝，则＝z2

    C．若|z1|＝|z2|，则z1·＝z2·

    D．若|z1|＝|z2|，则＝

     

    D

    【解析】A，|z1－z2|＝0⇒z1－z2＝0⇒z1＝z2⇒＝，真命题；

    B，z1＝⇒＝＝z2，真命题；

    C，|z1|＝|z2|⇒|z1|2＝|z2|2⇒z1·＝z2·，真命题；

    D，当|z1|＝|z2|时，可取z1＝1，z2＝i，显然＝1，＝－1，即≠，假命题．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学人教版评估检测 第三章 三角函数、解三角形（解析版） 题型：选择题

    函数y=cos2的图象沿x轴向右平移a个单位(a>0),所得图象关于y轴对称,则a的最小值为(　　)

    A.π B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数（解析版） 题型：填空题

    已知符号函数sgn(x)＝则函数f(x)＝sgn(ln x)－ln2x的零点个数为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 解析几何（解析版） 题型：填空题

    三角形ABC中，已知·＋·＋·＝－6，且角C为直角，则角C的对边c的长为__________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 解析几何（解析版） 题型：选择题

    直线l过抛物线C：x2＝4y的焦点且与y轴垂直，则l与C所围成的图形的面积等于(　　)

    A. B．2 C. D.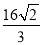

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：解答题

    已知数列{an}的前n项和为Sn，且Sn＝2an－2，数列{bn}满足b1＝1，且bn＋1＝bn＋2.

    (1)求数列{an}，{bn}的通项公式；

    (2)设cn＝an－bn，求数列{cn}的前2n项和T2n.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：填空题

    关于直线m，n和平面α，β有以下四个命题：

    ①若m∥α，n∥β，α∥β，则m∥n；

    ②若m∥n，m?α，n⊥β，则α⊥β；

    ③若α∩β＝m，m∥n，则n∥α且n∥β；

    ④若m⊥n，α∩β＝m，则n⊥α或n⊥β.

    其中假命题的序号是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 概率与统计（解析版） 题型：解答题

    为调查某社区居民的业余生活状况，研究这一社区居民在20：00－22：00时间段的休闲方式与性别的关系，随机调查了该社区80人，得到下面的数据表：

    休闲方式

    性别

    看电视

    看书

    合计

    男

    10

    50

    60

    女

    10

    10

    20

    合计

    20

    60

    80

     

    (1)将此样本的频率估计为总体的概率，随机调查3名在该社区的男性，设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X，求X的分布列和数学期望；

    (2)根据以上数据，我们能否在犯错误的概率不超过0．01的前提下，认为“在20：00－22：00时间段居民的休闲方式与性别有关系”？

    参考公式：K2＝，其中n＝a＋b＋c＋d．

    参考数据：

    P(K2≥k0)

    0．15

    0．10

    0．05

    0．025

    0．010

    k0

    2．072

    2．706

    3．841

    5．024

    6．635

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量（解析版） 题型：填空题

    已知点A(1，－1)，B(3,0)，C(2,1)．若平面区域D由所有满足＝λ＋μ(1≤λ≤2,0≤μ≤1)的点P组成，则D的面积为________．

     

    查看答案和解析>>

    同步练习册答案