
分析 (1)利用函数f(x)=$\frac{x^2}{{1+{x^2}}}$,代入计算,可得结论;
(2)利用$f(x)+\frac{1}{x^2}f(x)=\frac{x^2}{{1+{x^2}}}({1+\frac{1}{x^2}})=1$,$f(x)+f(\frac{1}{x})=1$,即可得出结论.
解答 解:(1)∵$f(x)=\frac{x^2}{{1+{x^2}}}$,
∴$f(2)+f(\frac{1}{2})=\frac{2^2}{{1+{2^2}}}+\frac{{{{(\frac{1}{2})}^2}}}{{1+{{(\frac{1}{2})}^2}}}=\frac{2^2}{{1+{2^2}}}+\frac{1}{{1+{2^2}}}=1$,
同理可得$f(3)+f(\frac{1}{3})=1,f(4)+f(\frac{1}{4})=1$.---------------------------(4分)
猜想$f(x)+f(\frac{1}{x})=1$.-------------------------(6分)
(2)∵$f(x)+\frac{1}{x^2}f(x)=\frac{x^2}{{1+{x^2}}}({1+\frac{1}{x^2}})=1$,-------------------------(8分)
又由(1)得,$f(x)+f(\frac{1}{x})=1$,则$\begin{array}{l}2f(2)+2f(3)+…+2f(2015)+f(\frac{1}{2})+f(\frac{1}{3})+…+f(\frac{1}{2015})+\frac{1}{2^2}f(2)+\frac{1}{3^2}f(3)+…+\frac{1}{{{{2015}^2}}}f(2015)\\=[f(2)+f(\frac{1}{2})+f(2)+\frac{1}{2^2}f(2)]+[f(3)+f(\frac{1}{3})+f(3)+\frac{1}{3^2}f(3)]+…+[f(2015)+f(\frac{1}{2015})+f(2015)+\frac{1}{{{{2015}^2}}}f(2015)]\end{array}$=$\underbrace{2+2+…+2}_{2014个2}=4028$.-----------------------------------------------------(12分)
点评 本题考查归纳推理,考查学生的计算能力,正确归纳是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{π}{2}$) | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | ($\frac{π}{4}$,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
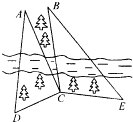 如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).
如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{7}^{4}$ | B. | C${\;}_{8}^{4}$ | C. | C${\;}_{8}^{3}$ | D. | C${\;}_{9}^{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com