
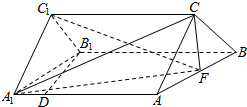
 已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为边长为1的正三角形,且AA1=2,D为AA1上的点,且A1D=$\frac{1}{4}$,F为AB的中点.
已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为边长为1的正三角形,且AA1=2,D为AA1上的点,且A1D=$\frac{1}{4}$,F为AB的中点.分析 (1)可取A1B1的中点E,并连接FE,根据条件可知FB,FE,FC三直线两两垂直,从而分别以这三直线为x,y,z轴,建立空间直角坐标系,然后可求出图形上一些点的坐标,从而得出$\overrightarrow{{B}_{1}D}$,$\overrightarrow{{A}_{1}C}$的坐标,容易得出$\overrightarrow{{B}_{1}D}•\overrightarrow{{A}_{1}C}=0$,从而证出B1D⊥A1C;
(2)可以求出向量$\overrightarrow{{A}_{1}{C}_{1}},\overrightarrow{F{A}_{1}},\overrightarrow{FC}$的坐标,可设平面A1CF的法向量为$\overrightarrow{m}=(x,y,z)$,根据$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{F{A}_{1}}=0}\\{\overrightarrow{m}•\overrightarrow{FC}=0}\end{array}\right.$即可求出法向量$\overrightarrow{m}$的坐标,可设直线A1C1与平面A1CF所成角为θ,从而根据$sinθ=|cos<\overrightarrow{{A}_{1}{C}_{1}},\overrightarrow{m}>|$即可求出sinθ的值.
解答 解:(1)证明:取A1B1的中点E,连接EF,则:FB,FE,FC三直线两两垂直,分别以这三直线为x,y,z轴,建立空间直角坐标系,则: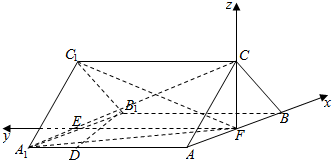
F(0,0,0),${B}_{1}(\frac{1}{2},2,0),D(-\frac{1}{2},\frac{7}{4},0),{A}_{1}(-\frac{1}{2},2,0)$,$C(0,0,\frac{\sqrt{3}}{2})$,${C}_{1}(0,2,\frac{\sqrt{3}}{2})$;
∴$\overrightarrow{{B}_{1}D}=(-1,-\frac{1}{4},0),\overrightarrow{{A}_{1}C}=(\frac{1}{2},-2,\frac{\sqrt{3}}{2})$;
∴$\overrightarrow{{B}_{1}D}•\overrightarrow{{A}_{1}C}=-\frac{1}{2}+\frac{1}{2}+0=0$;
∴$\overrightarrow{{B}_{1}D}⊥\overrightarrow{{A}_{1}C}$;
∴B1D⊥A1C;
(2)$\overrightarrow{F{A}_{1}}=(-\frac{1}{2},2,0),\overrightarrow{FC}=(0,0,\frac{\sqrt{3}}{2})$,$\overrightarrow{{A}_{1}{C}_{1}}$=$(\frac{1}{2},0,\frac{\sqrt{3}}{2})$;
设平面A1CF的法向量为$\overrightarrow{m}=(x,y,z)$,则:
$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{F{A}_{1}}=-\frac{1}{2}x+2y=0}\\{\overrightarrow{m}•\overrightarrow{FC}=\frac{\sqrt{3}}{2}z=0}\end{array}\right.$;
取y=1,则x=4,z=0,∴$\overrightarrow{m}=(4,1,0)$;
设直线A1C1和平面A1CF所成角为θ,则:
$sinθ=|cos<\overrightarrow{{A}_{1}{C}_{1}},\overrightarrow{m}>|$=$\frac{2}{1•\sqrt{17}}=\frac{2\sqrt{17}}{17}$;
即直线A1C1和平面A1CF所成角的正弦值为$\frac{2\sqrt{17}}{17}$.
点评 考查通过建立空间直角坐标系,利用空间向量解决异面直线垂直和线面角等问题的方法,能求空间点的坐标,数量积的坐标运算,向量垂直的充要条件,以及平面法向量的概念及求法,向量夹角余弦的坐标公式,清楚直线和平面所成角与直线的方向向量和平面法向量夹角的关系.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆的一部分 | B. | 双曲线的一部分 | C. | 抛物线的一部分 | D. | 圆的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
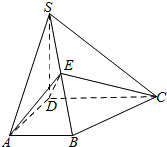 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,SD=2,E为棱SB上的一点,且SE=2EB,CE与平面SAB所成角的正弦值为$\frac{\sqrt{30}}{10}$.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,SD=2,E为棱SB上的一点,且SE=2EB,CE与平面SAB所成角的正弦值为$\frac{\sqrt{30}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com