
分析 (1)设A(rcosθ,rsinθ)、B(kcosα,ksinα),则r=|$\overrightarrow{OA}$|,k=|$\overrightarrow{OB}$|,将A,B代入椭圆方程,再由向量垂直的坐标表示,结合和角及同角的平方关系,化简整理即可得证;
(2)运用三角形的面积公式和勾股定理,化简整理可得|$\overrightarrow{OP}$|=$\frac{6\sqrt{13}}{13}$,即可得到P的轨迹.
解答 证明:(1)设A(rcosθ,rsinθ)、B(kcosα,ksinα),
则r=|$\overrightarrow{OA}$|,k=|$\overrightarrow{OB}$|,
点A在椭圆上,即有$\frac{{r}^{2}co{s}^{2}θ}{4}$+$\frac{{r}^{2}si{n}^{2}θ}{9}$=1,可得
$\frac{1}{{r}^{2}}$=$\frac{co{s}^{2}θ}{4}$+$\frac{si{n}^{2}θ}{9}$;
由$\overrightarrow{OA}$•$\overrightarrow{OB}$=0得,cosθcosα+sinθsinα=0,即为cos(θ-α)=0,
即有cos2α=sin2θ,cos2θ=sin2α.
同理可得,$\frac{1}{{k}^{2}}$=$\frac{co{s}^{2}α}{4}$+$\frac{si{n}^{2}α}{9}$.
所以$\frac{1}{|{\overrightarrow{OA}|}^{2}}$+$\frac{1}{|{\overrightarrow{OB}|}^{2}}$=$\frac{si{n}^{2}α+co{s}^{2}α}{4}$+$\frac{co{s}^{2}α+si{n}^{2}α}{9}$
=$\frac{1}{4}$+$\frac{1}{9}$=$\frac{13}{36}$为定值;
(2)由三角形面积公式,得|$\overrightarrow{OP}$|•|$\overrightarrow{AB}$|=|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|,
所以|$\overrightarrow{OP}$|2•|$\overrightarrow{AB}$|2=|$\overrightarrow{OA}$|2•|$\overrightarrow{OB}$|2,
由勾股定理可得,|$\overrightarrow{OP}$|2•(|$\overrightarrow{OA}$|2+|$\overrightarrow{OB}$|2)=|$\overrightarrow{OA}$|2•|$\overrightarrow{OB}$|2,
即有|$\overrightarrow{OP}$|2•($\frac{1}{|{\overrightarrow{OA}|}^{2}}$+$\frac{1}{|{\overrightarrow{OB}|}^{2}}$)=1,
由(1)可得|$\overrightarrow{OP}$|2•$\frac{13}{36}$=1,即为|$\overrightarrow{OP}$|=$\frac{6\sqrt{13}}{13}$.
则点P在以原点为圆心,$\frac{6\sqrt{13}}{13}$为半径的圆上.
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
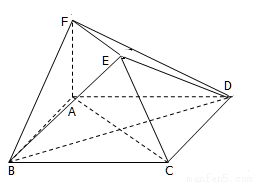
如图所示的多面体中,已知菱形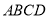 和直角梯形
和直角梯形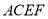 所在的平面互相垂直,其中
所在的平面互相垂直,其中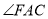 为直角,
为直角,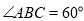 ,
,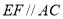 ,
,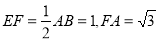 .
.
(1)求证: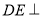 平面
平面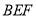 ;
;
(2)求多面体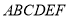 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
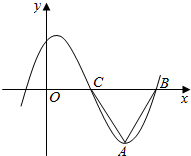 已知向量$\overrightarrow{a}$=(2cos$\frac{ωx}{2}$,$\sqrt{3}$),$\overrightarrow{b}$=(3cos$\frac{ωx}{2}$,sinωx),ω>0,设函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-3的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且△ABC为等边三角形,其高为2$\sqrt{3}$.
已知向量$\overrightarrow{a}$=(2cos$\frac{ωx}{2}$,$\sqrt{3}$),$\overrightarrow{b}$=(3cos$\frac{ωx}{2}$,sinωx),ω>0,设函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-3的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且△ABC为等边三角形,其高为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 无数个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com