
����Ŀ����֪���з�����״��С��ͬ��С�����ɣ����б��Ϊ0��С��1�������Ϊ1��С��1�������Ϊ2��С��![]() �����Ӵ��������ȡһ��С��ȡ�����Ϊ2��С��ĸ���Ϊ
�����Ӵ��������ȡһ��С��ȡ�����Ϊ2��С��ĸ���Ϊ![]() ���ִӴ��в��Żص����ȡ��2��С�ǵ�һ��ȡ����С����Ϊ
���ִӴ��в��Żص����ȡ��2��С�ǵ�һ��ȡ����С����Ϊ![]() ���ڶ���ȡ����С����Ϊ
���ڶ���ȡ����С����Ϊ![]() .
.
��1���ǡ�![]() ��Ϊ�¼�
��Ϊ�¼�![]() �����¼�
�����¼�![]() �����ĸ���.
�����ĸ���.
��2��������![]() ����ȡ����ʵ��
����ȡ����ʵ��![]() �����¼�
�����¼�![]() ��
��![]() ��������ĸ���.
��������ĸ���.
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�Ķ������У� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��![]() ���е�.
���е�.

(1)��֤�� ![]() ƽ��
ƽ��![]() ��
��
(2)������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����DD������������Ϊ������Ⱥ�ṩ��ݾ��á���ɫ��̼�Ļ������з�ʽ������Ŀǰ�������е�Ͷ������ʹ�õ�������������˳������飬��ȡ�����ڶ�ʮ����ʮ��IJ�ͬ�Ա�������ߣ�ͳ���������±���ʾ��
���� | Ů�� | �ϼ� | |
20��35�� |
| 40 | 100 |
36��50�� | 40 |
| 90 |
�ϼ� | 100 | 90 | 190 |
(1)��ͳ�����ݱ���![]() ��ֵ��
��ֵ��
(2)�����ó鵽��100��20��35���������������Ϊ��������ȫ�еĸ��������Ůʹ�á�DD����������������ִ�ȫ�еĸ�������������������ȡ3�ˣ���ǡ��һ��Ů�Եĸ��ʣ�
(3)�����������������ж�ʹ�á�DD��������������Ⱥ�У��ܷ���![]() �İ�����Ϊ���Ա��롰���䡱�йأ���˵������.
�İ�����Ϊ���Ա��롰���䡱�йأ���˵������.
�������
|
|
|
|
|
|
|
|
|
|
�ο���ʽ�� 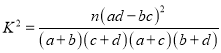 ��
�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ,
, ![]() .
.
��������![]() ʱ��������
ʱ��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��������![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
��������![]() ʱ������
ʱ������![]() ��
��![]() �ϵ����ֵΪ
�ϵ����ֵΪ![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������ʵ��b��ȡֵ��Χ.
��������ʵ��b��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˺��������Ļ���ijУ�����ˡ��Ұ���ѧ�����о��䡱���ԣ������������ȡ��100�������ijɼ����÷־�Ϊ����,����100�֣�����ͳ���Ʊ������гɼ�������80�ֵĿ�������Ϊ�������������Ƶ�ʷֲ��������ṩ�����ݣ���Ƶ�ʹ��Ƹ��ʣ��ش���������.
���� | Ƶ�� | Ƶ�� |
| 5 | 0.05 |
|
| 0.20 |
| 35 |
|
| 25 | 0.25 |
| 15 | 0.15 |
�ϼ� | 100 | 1.00 |
��1����![]() ��ֵ��������100�������ɼ���ƽ���֣�
��ֵ��������100�������ɼ���ƽ���֣�
��2����Ƶ�ʷֲ����еijɼ����飬���÷ֲ������ȡ20�˲μ�ѧУ�ġ��Ұ���ѧ�����������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ��������
��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2��������![]() ���䶨������Ϊ����������
���䶨������Ϊ����������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���ڣ�2���������£��躯��![]() ������
������![]() �����ٴ���һ��
�����ٴ���һ��![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ���������غϵ�ֱ�ߣ�
���������غϵ�ֱ�ߣ� ![]() ���������غϵ�ƽ�棬�����������⣺
���������غϵ�ƽ�棬�����������⣺
����![]() ��
�� ![]() ����
����![]() ��
��
����![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
��
����![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
��
�ܵ�![]() ����
����![]() ʱ����
ʱ����![]() ����
����![]() .
.
������ȷ����ĸ�����( )
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���οʹ�ij���ξ����ľ���A����ɽ��C��������·����һ���Ǵ�A��ֱ�߲��е�C����һ�����ȴ�A���������³���B��Ȼ���B��ֱ�߲��е�C��
���мס�����λ�οʹ�A����ɽ������AC���ٲ��У��ٶ�Ϊ50 m/min���ڼ׳���2 min���Ҵ�A���³���B����B��ͣ��1 min���ٴ�B���ٲ��е�C�������³�����ֱ�����е��ٶ�Ϊ130 m/min��ɽ·AC��Ϊ1 260 m����������cos A��![]() ��cos C��
��cos C��![]() ��
��
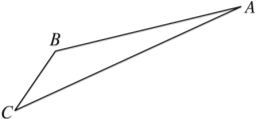
��1��������AB�ij���
��2�����ҳ������ٷ��Ӻ������³�����ľ�����̣�
��3��Ϊʹ��λ�ο���C������ȴ���ʱ�䲻����3���ӣ��Ҳ��е��ٶ�Ӧ������ʲô��Χ�ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ΪR�ĺ���f��x��= ![]() ���溯����
���溯����
��1����f��x���Ľ���ʽ��
��2����������t��R������ʽf��t2��2t��+f��2t2��k����0���������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com