
分析 (1)通过将点(n,Sn)代入函数y=2n+r(r为常数)方程,利用an=Sn-Sn-1可知数列{an}的通项公式,进而可知列{bn}的通项公式;
(2)通过(1)裂项可知cn=1+($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)(n≥2),进而并项相加,分类讨论即得结论.
解答 解:(1)∵点(n,Sn)均在函数y=2n+r(r为常数)的图象上,
∴Sn=2n+r,
当n≥2时,an=Sn-Sn-1=2n-1,
∴an=$\left\{\begin{array}{l}{2+r,}&{n=1}\\{{2}^{n-1},}&{n≥2}\end{array}\right.$;
∵bn=2(log2an+1)(n∈N*),
∴bn=$\left\{\begin{array}{l}{2(lo{g}_{2}(2+r)+1),}&{n=1}\\{2n,}&{n≥2}\end{array}\right.$;
(2)由(1)可知cn=$\frac{{{b}_{n}}^{2}+1}{{{b}_{n}}^{2}-1}$=1+($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)(n≥2),
当n≥2时,Tn-T1=c2+c3+…+cn
=(n-1)+1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$
=n-$\frac{1}{2n+1}$,
∴Tn=$\left\{\begin{array}{l}{{c}_{1},}&{n=1}\\{{c}_{1}+n-\frac{1}{2n+1},}&{n≥2}\end{array}\right.$,
其中c1=$\frac{{{b}_{1}}^{2}+1}{{{b}_{1}}^{2}-1}$=$\frac{4[lo{g}_{2}(2+r)]^{2}+8lo{g}_{2}(2+r)+5}{4[lo{g}_{2}(2+r)^{2}]^{2}+8lo{g}_{2}(2+r)+3}$.
点评 本题考查数列的通项及前n项和,考查分类讨论的思想,考查裂项相消法,注意解题方法的积累,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
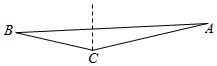 如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.
如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com