
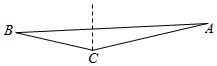
 如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.
如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里. 分析 使用正弦定理解出sinB,根据内角和定理得出sinA,再次使用正弦定理解出BC.
解答 解:由题意知∠ACB=75°+75°=150°,AC=3,AB=$\sqrt{21}$.
由正弦定理得$\frac{AB}{sin∠ACB}=\frac{AC}{sinB}$,即$\frac{\sqrt{21}}{sin150°}=\frac{3}{sinB}$,解得sinB=$\frac{\sqrt{21}}{14}$.
∴cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{5\sqrt{7}}{14}$.
∴sinA=sin(B+C)=sinBcosC+cosBsinC=$\frac{\sqrt{7}}{14}$.
由正弦定理得$\frac{BC}{sinA}=\frac{AB}{sin∠ACB}$,即$\frac{BC}{\frac{\sqrt{7}}{14}}=\frac{\sqrt{21}}{\frac{1}{2}}$,解得BC=$\sqrt{3}$.
故答案为$\sqrt{3}$海里.
点评 本题考查了正弦定理在解三角形的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1} | B. | {x|x<1} | C. | {x|x>0} | D. | {x|x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com