
分析 (1)根据直线l1、l2的方程,讨论a的取值,求出直线l1、l2的斜率,利用二倍角的正切值列出方程,求出a的值;
(2)求出直线l1、l2交点的横坐标,再求出直线l1、l2与y轴交点的纵坐标,写出直线l1、l2与y轴围成三角形的面积,列出方程求出a的值.
解答 解:(1)直线l1:2x-(a-1)y+1=0,l2:2ax+(a+1)y+a=0(a∈R).
令a-1=0,得a=1,此时直线l1的倾斜角是$\frac{π}{2}$,
直线l2的方程为2x+2y+1=0,倾斜角是$\frac{3π}{4}$,不满足题意;
同理可得a≠-1;
当a≠±1时,直线l1的斜率为k1=$\frac{2}{a-1}$,直线l2的斜率为k2=-$\frac{2a}{a+1}$;
由题意,k2=$\frac{{2k}_{1}}{1{{-k}_{1}}^{2}}$,
即-$\frac{2a}{a+1}$=$\frac{2×\frac{2}{a-1}}{1{-(\frac{2}{a-1})}^{2}}$,
化简得a2-a-2=0,
解得a=2或a=-1(不合题意,舍去),
所以a的值为2;
(2)由l1、l2组成方程组$\left\{\begin{array}{l}{2x-(a-1)y+1=0}\\{2ax+(a+1)y+a=0}\end{array}\right.$,
解得x=-$\frac{1}{2}$;
又直线l1与y轴的交点为(0,$\frac{1}{a-1}$),
直线l2与y轴的交点为(0,-$\frac{a}{a+1}$),
所以直线l1、l2与y轴围成的三角形面积为
$\frac{1}{2}$×|-$\frac{1}{2}$|×|$\frac{1}{a-1}$+$\frac{a}{a+1}$|=$\frac{1}{2}$,
解得a=±$\sqrt{3}$或a=±$\frac{\sqrt{3}}{3}$.
点评 本题考查了直线方程的应用问题,也考查了方程组的解法与应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
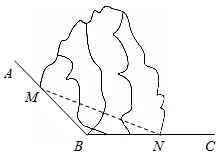 如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).
如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
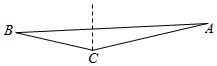 如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.
如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com