
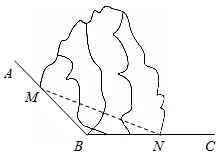
 如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).
如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).分析 (1)利用余弦定理列方程解出;
(2)根据正弦定理用θ表示出BN,BM,使用和角公式化简L,根据θ的范围和正弦函数的性质得出L的最大值.
解答 解:(1)设BM=x,则BN=x-4,MN=x+4,
在△MBN中,由余弦定理得MN2=BN2+BM2-2BN•BMcosB,
即(x+4)2=(x-4)2+x2+x(x-4),解得x=10.
∴MN=x+4=14(千米).
(2)∠BMN=60°-θ,
由正弦定理得$\frac{BM}{sinθ}=\frac{BN}{sin(60°-θ)}=\frac{MN}{sin120°}$=8$\sqrt{3}$,
∴BM=8$\sqrt{3}$sinθ,BN=8$\sqrt{3}$sin(60°-θ)
∴L=BM+BN+MN=8$\sqrt{3}$sinθ+8$\sqrt{3}$sin(60°-θ)+12=12cosθ+4$\sqrt{3}$sinθ+12=8$\sqrt{3}$sin(θ+60°)+12.
∵0<θ<60°,∴60°<θ+60°<120°.
∴当θ+60°=90°时,L取得最大值8$\sqrt{3}+12$千米.
点评 本题考查了正余弦定理在解三角形中的应用,三角函数的恒等变换,正弦函数的图象与性质,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,把f(x)的图象上各点向左平移$\frac{1}{2}$单位,得到函数g(x)的图象,则g($\frac{5}{2}$)=( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,把f(x)的图象上各点向左平移$\frac{1}{2}$单位,得到函数g(x)的图象,则g($\frac{5}{2}$)=( )| A. | -1 | B. | 1 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1} | B. | {x|x<1} | C. | {x|x>0} | D. | {x|x<0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com