
分析 通过分母有理化、裂项可知$\frac{1}{\sqrt{n}+\sqrt{n+2}}$=$\frac{1}{2}$($\sqrt{n+2}$-$\sqrt{n}$),进而并项相加即得结论.
解答 解:∵$\frac{1}{\sqrt{n}+\sqrt{n+2}}$=$\frac{\sqrt{n+2}-\sqrt{n}}{(\sqrt{n}+\sqrt{n+2})(\sqrt{n+2}-\sqrt{n})}$=$\frac{1}{2}$($\sqrt{n+2}$-$\sqrt{n}$),
∴Sn=$\frac{1}{2}$($\sqrt{3}$-1+$\sqrt{4}$-$\sqrt{2}$+…+$\sqrt{n+2}$-$\sqrt{n}$)
=$\frac{1}{2}$(-1-$\sqrt{2}$+$\sqrt{n+1}$+$\sqrt{n+2}$).
点评 本题考查数列的求和,考查裂项相消法,注意解题方法的积累,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
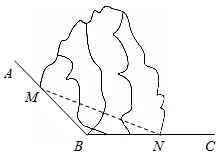 如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).
如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
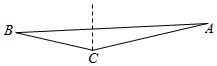 如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.
如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com