
分析 1)根据题意,分析可得,将n 表示n=a0×2k+a1×2k-1+a2×2k-2+…+ak-1×21+ak×20,实际是将十进制的数转化为二进制的数,易得12=1×23+1×22+0×21+0×20,由I(n)的意义,可得答案;
(2)由组合数的性质,分析其中I(n)的取值情况,与二项式定理结合,可转化为等比数列的前7项和,计算可得答案.
解答 解:(1)根据题意,12=1×23+1×22+0×21+0×20,则I(12)=2;
(2)I(1)=0=0•2-1,I(2)+I(3)=1=1•20,
I(4)+I(5)+I(6)+I(7)=4=2•21,
I(8)+I(9)+…+I(15)=12=3•22…,
所以I(1)+I(2)+…+I(2048)
=0•2-1+1•20+2•21+…+10•29+11=9228,
故答案为:2,9228.
点评 解本题关键在于分析题意,透彻理解I(n)的含义的运算,注意转化思想,结合二项式定理与等比数列的前n项和公式进行计算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 0或 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
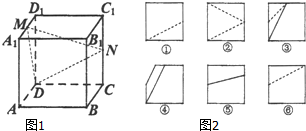
| A. | ①④⑤ | B. | ②③⑥ | C. | ①③⑤ | D. | ②④⑥ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (-1,-4) | C. | (1,0)或(-1,-4) | D. | (1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆锥SO中,AB、CD为底面圆O的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,P为SB的中点.(1)求证:SA∥平面PCD;
如图,圆锥SO中,AB、CD为底面圆O的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,P为SB的中点.(1)求证:SA∥平面PCD;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com