
已知数列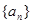 满足
满足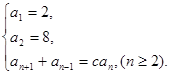 (
(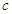 为常数,
为常数,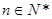 )
)
(1)当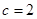 时,求
时,求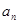 ;
;
(2)当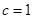 时,求
时,求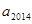 的值;
的值;
(3)问:使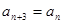 恒成立的常数
恒成立的常数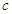 是否存在?并证明你的结论.
是否存在?并证明你的结论.
(1)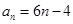 ;(2)
;(2) ;(3)存在
;(3)存在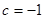
解析试题分析:(1)由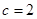 ,所以
,所以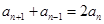 ,
,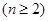 .所以数列
.所以数列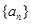 是一个等差数列.首项为2,公差为6,所以可求得通项公式.
是一个等差数列.首项为2,公差为6,所以可求得通项公式.
(2)由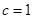 ,由于需要求
,由于需要求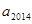 的值,所以考虑数列
的值,所以考虑数列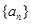 的周期性,通过列举即可得到数列
的周期性,通过列举即可得到数列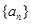 的周期为6.从而可求得
的周期为6.从而可求得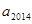 的值.
的值.
(3)假设存在常数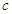 使得
使得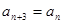 恒成立.由
恒成立.由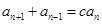 ,向前递推一个式子,再利用
,向前递推一个式子,再利用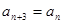 将得到两个关于
将得到两个关于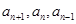 的等式,从而消去一个即可得到
的等式,从而消去一个即可得到 ,或
,或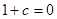 .由于
.由于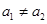 .所以只有
.所以只有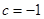 .再结合已知即可得到结论.
.再结合已知即可得到结论.
试题解析:(1)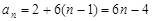
(2)  ,
, ,
,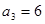 ,
, ,
,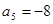 ,
,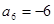 ,
, ,
, ,
, ,
,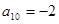 ,
,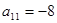 ,
,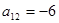 ,我们发现数列为一周期为6的数列.事实上,由
,我们发现数列为一周期为6的数列.事实上,由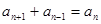 有
有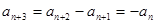 ,
, .……8分(理由和结论各2分)
.……8分(理由和结论各2分)
因为 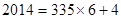 ,所以
,所以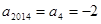 .
.
(3)假设存在常数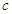 ,使
,使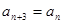 恒成立.
恒成立.
由 ①,
①,
及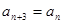 ,有
,有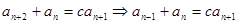 ②
②
1式减2式得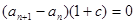 .
.
所以 ,或
,或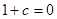 .
.
当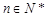 ,
, 时,数列{
时,数列{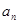 }为常数数列,不满足要求.
}为常数数列,不满足要求.
由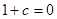 得
得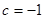 ,于是
,于是 ,即对于
,即对于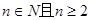 ,都有
,都有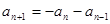 ,所以
,所以 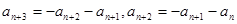 ,从而
,从而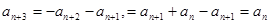
 .
.
所以存在常数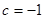 ,使
,使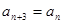 恒成立.
恒成立.
考点:1.等差数列的判断.2.数列的周期性.3.数列恒成立问题.4.递推的思想.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com