Question

14．如图，在三棱锥P-ABC中，AC=BC=$\sqrt{2}$，∠ACB=90°，AP=BP=AB，PC⊥AC．
（1）求二面角B-AP-C的正切值；
2）求点C到平面APB的距离．

Answer 1

分析 （1）推导出PC⊥平面ABC，BC⊥平面PAC，BC⊥AP，设点E为棱PA的中点，连结BE，CE，则BE⊥AP，再推导出EC⊥AP，从而∠BEC是二面角B-AP-C的平面角，由此能求出二面角B-AP-C的正切值．
（2）以C为原点，CB为x轴，CA为y轴，CP为z轴，建立空间直角坐标系，利用向量法能求出点C到平面APB的距离．

解答 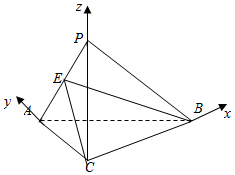解：（1）∵AC=BC=$\sqrt{2}$，AP=BP，PC=PC，
∴△APC≌△BPC，
又PC⊥AC，∴PC⊥BC
又∵AC∩BC=C，AC，BC?平面ABC，
∴PC⊥平面ABC，
∵PC⊥BC，BC⊥AC，PC∩AC=C，PC，AC?平面PAC
∴BC⊥平面PAC．
又∵AP?平面PAC，∴BC⊥AP，
设点E为棱PA的中点，连结BE，CE，
∵BP=AB，点E为棱PA中点，∴BE⊥AP．
又∵BC∩BE=B，BC，BE?平面BEC，∴PA⊥平面BEC，
∵EC?平面BEC，∴EC⊥AP，∴∠BEC是二面角B-AP-C的平面角，
AB=AP=AP=$\sqrt{2+2}$=2，在Rt△BCE中，BC=$\sqrt{2}$，BE=$\sqrt{4-1}$=$\sqrt{3}$，
∴tan∠BEC=$\frac{BC}{EC}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$．
∴二面角B-AP-C的正切值为$\frac{\sqrt{6}}{3}$．
（2）以C为原点，CB为x轴，CA为y轴，CP为z轴，建立空间直角坐标系，
C（0，0，0），A（0，$\sqrt{2}$，0），B（$\sqrt{2}，0，0$），P（0，0，$\sqrt{2}$），
$\overrightarrow{PA}$=（0，$\sqrt{2}，-\sqrt{2}$），$\overrightarrow{PB}$=（$\sqrt{2}，0，-\sqrt{2}$），$\overrightarrow{CP}$=（0，0，$\sqrt{2}$），
设平面PAB的法向量$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PA}=\sqrt{2}y-\sqrt{2}z=0}\\{\overrightarrow{n}•\overrightarrow{PB}=\sqrt{2}x-\sqrt{2}z=0}\end{array}\right.$，取x=1，得$\overrightarrow{n}$=（1，1，1），
∴点C到平面APB的距离d=$\frac{|\overrightarrow{CP}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$．

点评 本题考查的知识点是二面角的平面角及求法，考查点到平面的距离的求法，考查直线与平面垂直的判定及性质，熟练掌握空间线面垂直与线线垂直之间的转化及理解二面角的平面角的概念是解答的关键．