Question

4．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F₁、F₂，点P为椭圆C上一点，|PF₁|+|PF₂|=8$\sqrt{2}$，点F₁关于直线x+y=0的对称点A在椭圆上．
（1）求椭圆C的方程；
（2）设线段MN为圆C：x²+（y-3）²=1的直径，求$\overrightarrow{PM}$•$\overrightarrow{PN}$的取值范围．

Answer 1

分析 （1）通过|PF₁|+|PF₂|=8$\sqrt{2}$得a²=32，再利用点F₁（-c，0）关于直线x+y=0的对称点A为A（0，c）且A在椭圆上，得b²=16，即得椭圆C的方程；
（2）通过化简得$\overrightarrow{PM}•\overrightarrow{PN}$=${\overrightarrow{DP}}^{2}$-${\overrightarrow{DN}}^{2}$=$|\overrightarrow{DP}{|}^{2}$-$\frac{1}{4}$，联立圆D：x²+（y-3）²=t²与椭圆方程，消去x令△=0可得$|\overrightarrow{DP}|$的最大值为$5\sqrt{2}$，计算即可$\overrightarrow{PM}$•$\overrightarrow{PN}$的取值范围．

解答 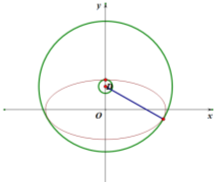解：（1）∵|PF₁|+|PF₂|=8$\sqrt{2}$，∴2a=$8\sqrt{2}$，即a²=32，
∵点F₁（-c，0）关于直线x+y=0的对称点A为A（0，c），且A在椭圆上，
∴$\frac{{c}^{2}}{{b}^{2}}=1$，即b²=c²，∴a²=b²+c²=2b²，∴b²=16，
∴椭圆C的方程为：$\frac{{x}^{2}}{32}+\frac{{y}^{2}}{16}=1$；
（2）记圆C：x²+（y-3）²=1的圆心为D（0，3），则点D在椭圆C的内部，
∴$\overrightarrow{PM}•\overrightarrow{PN}$=（$\overrightarrow{DM}-\overrightarrow{DP}$）•（$\overrightarrow{DN}-\overrightarrow{DP}$）=（$-\overrightarrow{DN}$$-\overrightarrow{DP}$）•（$\overrightarrow{DN}-\overrightarrow{DP}$）=${\overrightarrow{DP}}^{2}$-${\overrightarrow{DN}}^{2}$，
∵${\overrightarrow{DN}}^{2}=|\overrightarrow{DN}{|}^{2}$=$\frac{1}{4}$，∴$\overrightarrow{PM}•\overrightarrow{PN}$=$|\overrightarrow{DP}{|}^{2}$-$\frac{1}{4}$，
设圆D：x²+（y-3）²=t²，联立圆D与椭圆方程，消去x，得y²+6y+t²-41=0，
令△=36-4（t²-41）=0，解得t²=50，
∴点P为圆D：x²+（y-3）²=50与椭圆的交点时距离D点最远为$5\sqrt{2}$，且
圆C：x²+（y-3）²=1与椭圆的交点（0，3）距离D点最近，
∴$1≤|\overrightarrow{DP}{|}^{2}≤50$，$\frac{3}{4}≤$$|\overrightarrow{DP}{|}^{2}$$≤\frac{199}{4}$，
∴$\overrightarrow{PM}$•$\overrightarrow{PN}$的取值范围为$[\frac{3}{4}，\frac{199}{4}]$．

点评 本题考查圆锥曲线的简单性质，圆与椭圆的位置关系，点到直线的距离公式，向量的数量积运算，向量的加、减法运算法则，考查分析问题、解决问题的能力，属于难题．