
| A. | 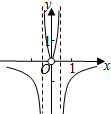 | B. | 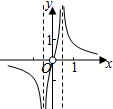 | C. | 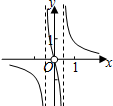 | D. | 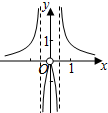 |
分析 判断奇偶性排除B,C,再利用特殊函数值判断即可得出答案.
解答 解:∵y=f(x)=$\frac{1}{{ln|{e^x}-{e^{-x}}|}}$,
∴f(-x)=$\frac{1}{ln|{e}^{-x}-{e}^{x}|}$=$\frac{1}{{ln|{e^x}-{e^{-x}}|}}$=f(x),
∴f(x)是偶函数,图象关于y轴对称,
所以排除B,C.
∵f(2)=$\frac{1}{ln|{e}^{2}-{e}^{-2}|}$>0,
∴(2,f(2))在x轴上方,所以排除A,
故选:D.
点评 本题考查了对数,指数函数的性质,奇函数的偶函数的图象性质,考查了学生对于函数图象的整体把握,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}\sqrt{5}$ | C. | $\sqrt{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,ex-x-1>0 | B. | ?x∉R,ex-x-1>0 | C. | ?x∈R,ex-x-1≥0 | D. | ?x∈R,ex-x-1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [0,1] | C. | [-1,2] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
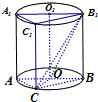 如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P
如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com