��������������⣺
��ij�༶һ����52��ѧ�����ֽ��ð�ѧ�������ţ���ϵͳ�����ķ�����ȡһ������Ϊ4����������֪7�ţ�33�ţ�46��ͬѧ�������У���ô������һλͬѧ�ı��Ϊ23��
��һ������1��2��3��4��5��ƽ��������������λ����ͬ��
��һ������a��0��1��2��3�����������ݵ�ƽ��ֵΪ1������������Ϊ2��
�ܸ��ݾ���������ع�ϵ������������ͳ���������õĻع�ֱ�߷���Ϊ
=ax+b��b=2��
=1��
=3����a=1��
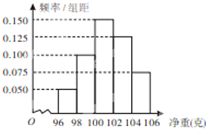
����ͼ�Ǹ��ݳ�������ó��IJ�Ʒ�������أ���λ���ˣ����ݻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ����֪�����в�Ʒ����С��100�˵ĸ�����36���������о��ش��ڻ����98�ˣ�����С��104�˵IJ�Ʒ�ĸ�����90��
������������������
| A���٢ڢ� | B���ڢܢ� |
| C���ڢۢ� | D���ۢܢ� |
|

 ��������������⣺
��������������⣺

 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
 ��ͼ��������P-ABCD�У�����ABCDΪֱ�����Σ�AD��BC����ADC=90�㣬ƽ��PAD�͵���ABCD��QΪAD���е㣬M����PC�ϵĵ㣬PA=PD=2��BC=
��ͼ��������P-ABCD�У�����ABCDΪֱ�����Σ�AD��BC����ADC=90�㣬ƽ��PAD�͵���ABCD��QΪAD���е㣬M����PC�ϵĵ㣬PA=PD=2��BC=