
分析 (1)根据对数的运算性质化简即可,
(2)根据指数幂的运算性质化简即可.
解答 解:(1)原式=lg5(lg4+lg5)+(lg2)2=(lg5+lg2)2=1,
(2)原式=(-$\frac{3}{2}$)${\;}^{3×(-\frac{2}{3})}$+(2×10-3)${\;}^{{\;}^{\;}}$${\;}^{-\frac{1}{2}}$-$\frac{10}{\sqrt{5}-2}$+1=$\frac{4}{9}$+10$\sqrt{5}$-10($\sqrt{5}$+2)+1=-$\frac{167}{9}$
点评 本题考查了指数幂和对数的运算性质,属于基础题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
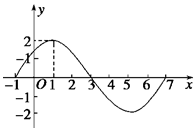 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10元 | B. | 15元 | C. | 20元 | D. | 25元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪P | B. | M∩P | C. | (∁UM)∪(∁∪P) | D. | (∁UM)∩(∁UP) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-|x-1| | B. | y=x2-2x+3 | C. | y=ln(x+1) | D. | y=2${\;}^{-\frac{x}{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com