
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①③ |
分析 由不等式的左边由210项,且小于$\frac{1}{{2}^{10}}$,即可判断①;运用绝对值不等式的性质,即可判断②;
运用基本不等式,即可判断③;运用不等式的放缩法,即可判断④.
解答 解:对于①,$\frac{1}{{2}^{10}}$+$\frac{1}{{2}^{10}+1}$+$\frac{1}{{2}^{10}+2}$+…+$\frac{1}{{2}^{11}-1}$<$\frac{1}{{2}^{10}}$+$\frac{1}{{2}^{10}}$+…+$\frac{1}{{2}^{10}}$=1,故①不正确;
对于②若|a|<1,则|a+b|-|a-b|≤|(b+a)-(b-a)|=2|a|<2,故②不正确;
对于③,lg9•lg11<($\frac{lg9+lg11}{2}$)2<$\frac{l{g}^{2}100}{4}$=1,故③正确;
对于④,若x>0,y>0,由$\frac{x}{1+x}$>$\frac{x}{1+x+y}$,$\frac{y}{1+y}$>$\frac{y}{1+x+y}$,
可得$\frac{x+y}{1+x+y}<\frac{x}{1+x}+\frac{y}{1+y}$,故④正确.
故选:A.
点评 本题考查命题的真假判断和运用,主要是不等式的放缩和基本不等式的运用,以及不等式的性质,考查推理能力和判断能力,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:选择题
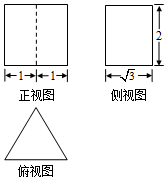
| A. | $\frac{4}{3}π$ | B. | $\frac{{32\sqrt{3}}}{27}π$ | C. | $\frac{{28\sqrt{3}}}{27}π$ | D. | $\frac{{28\sqrt{21}}}{27}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{42}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{41}{11}$ | D. | $\frac{6}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $\frac{3}{2}$ | C. | 3$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{7}{3}$ | C. | $\frac{13}{4}$ | D. | $\frac{43}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com